Good Morning,
I run a 3D non-linear analysis in Nastan using SOL106.
The volume is modeled with CTETRA elements while CTRIA3 exist on skin.
Part is loaded in traction.
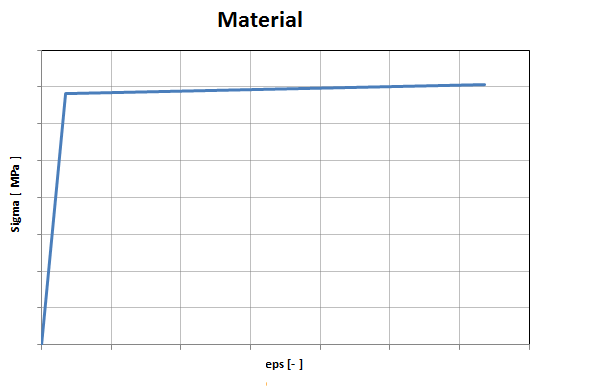
Material used is a steel for which an elasto-plastic curve - like the one shown here below - is used:
Further, MAT1 and MAST1 with PLASTIC option at field 4 is used.
I run 4 analyses:
- @ 50% of load
- @ 100% of load
- @ 150% of load
- @ 2000% of load
At critical site, I extracted Von Mises and Max principal stresses,(sigma1).
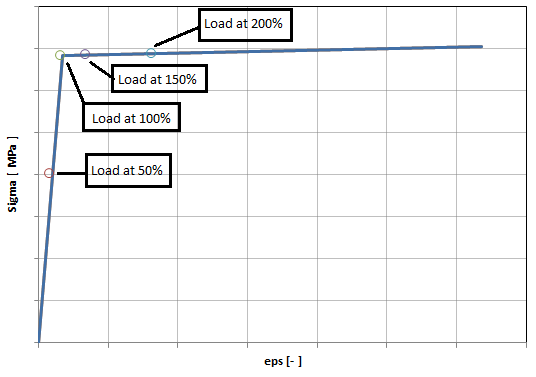
Here is what I get when I superpose Von Mises stresses on material curve.
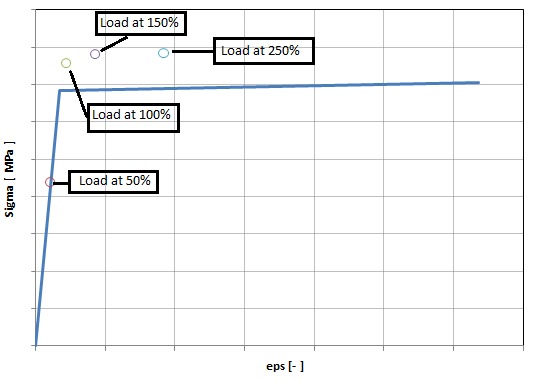
Here is what I get when I superpose principal stresses on material curve.
Could anyone explain why VM stress follows the curce and Principal stress does not, (in plastic region this is evident) ?
Do I need to rotate material properties in principal stress direction in the second graph?
Thank you for you help ans suggestions.
Marc
I run a 3D non-linear analysis in Nastan using SOL106.
The volume is modeled with CTETRA elements while CTRIA3 exist on skin.
Part is loaded in traction.
Material used is a steel for which an elasto-plastic curve - like the one shown here below - is used:
Further, MAT1 and MAST1 with PLASTIC option at field 4 is used.

I run 4 analyses:
- @ 50% of load
- @ 100% of load
- @ 150% of load
- @ 2000% of load
At critical site, I extracted Von Mises and Max principal stresses,(sigma1).
Here is what I get when I superpose Von Mises stresses on material curve.

Here is what I get when I superpose principal stresses on material curve.

Could anyone explain why VM stress follows the curce and Principal stress does not, (in plastic region this is evident) ?
Do I need to rotate material properties in principal stress direction in the second graph?
Thank you for you help ans suggestions.
Marc
