LeonhardEuler
Structural
- Jun 19, 2017
- 200
All,
Have a theory question about connection design and flexibility of connections.
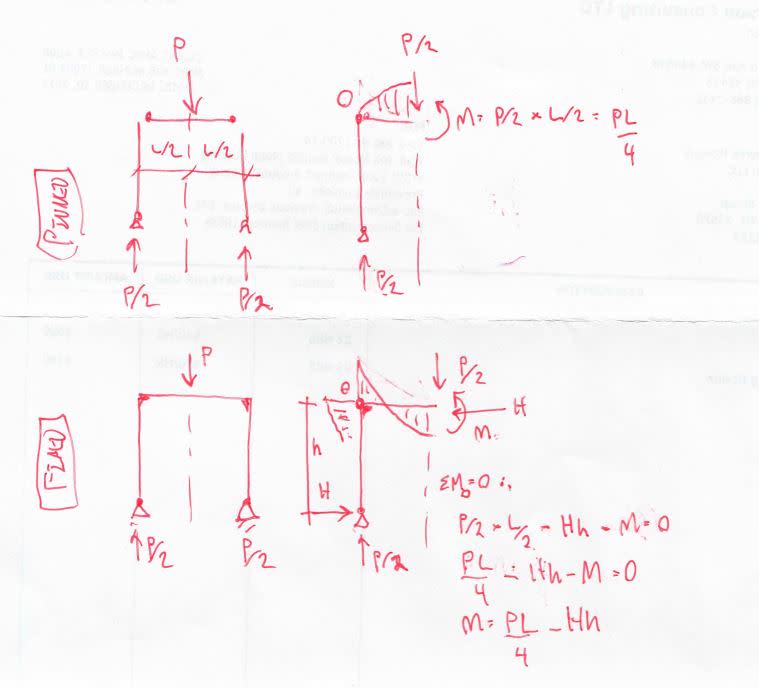
A connection was originally designed as a full moment connection, but FEM results came back and the connecting elements were not strong enough to carry the full end moment. The connection however is flexible and could be consider a partially restrained moment connection. The current idea is to replace the connection in the structural analysis program with a small member with an I equal to the connecting element and determine the new moment reaction at the node in question. This is done and the moment is lower and the FEM results show the connection passes. This is all good and seems to be allowable; however, I am having a little trouble with some of the theory behind this.
My main problem is that this is a "cantilever" connection which is being partially released about the vertical axis. I understand that a partial moment connection results in greater moment in the connecting member, but I feel that the force applied to the connecting beam must eventually make it into the column line, through the connecting element, so how can it have less of an internal moment? How is that "extra" force being transferred. Perhaps it is due to the connecting members stiffness and that it stops rotating past a certain angle and transmits remaining force as internal shear in the connecting element. I have found it extremely challenging to put my question into words, but hopefully someone will have success in explaining this to me. Thank you.
Have a theory question about connection design and flexibility of connections.
A connection was originally designed as a full moment connection, but FEM results came back and the connecting elements were not strong enough to carry the full end moment. The connection however is flexible and could be consider a partially restrained moment connection. The current idea is to replace the connection in the structural analysis program with a small member with an I equal to the connecting element and determine the new moment reaction at the node in question. This is done and the moment is lower and the FEM results show the connection passes. This is all good and seems to be allowable; however, I am having a little trouble with some of the theory behind this.
My main problem is that this is a "cantilever" connection which is being partially released about the vertical axis. I understand that a partial moment connection results in greater moment in the connecting member, but I feel that the force applied to the connecting beam must eventually make it into the column line, through the connecting element, so how can it have less of an internal moment? How is that "extra" force being transferred. Perhaps it is due to the connecting members stiffness and that it stops rotating past a certain angle and transmits remaining force as internal shear in the connecting element. I have found it extremely challenging to put my question into words, but hopefully someone will have success in explaining this to me. Thank you.