Navigation
Install the app
How to install the app on iOS
Follow along with the video below to see how to install our site as a web app on your home screen.
Note: This feature may not be available in some browsers.
More options
Style variation
-
Congratulations TugboatEng on being selected by the Eng-Tips community for having the most helpful posts in the forums last week. Way to Go!
You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Nreq in Table 10-6 of AISC manual 13 ed.
- Thread starter srm01
- Start date
- Status
- Not open for further replies.
jimstructures
Structural
srm01,
Are you kidding me???
Blodgett's Formula, circa 1985~ and Allowable Stress Design, AISC Red Book, 8th ed. or Green Book,9th ed.
AISC 13th Ed, 10-90 Table 10-6, LRFD or modified ASD.
Look for the formula for this table 10-6, in the footnotes or in the companion examples volume.
Good Luck.
Jim H
Are you kidding me???
Blodgett's Formula, circa 1985~ and Allowable Stress Design, AISC Red Book, 8th ed. or Green Book,9th ed.
AISC 13th Ed, 10-90 Table 10-6, LRFD or modified ASD.
Look for the formula for this table 10-6, in the footnotes or in the companion examples volume.
Good Luck.
Jim H
- Thread starter
- #3
Not kidding. I have not found the formula in the AISC Steel Manual. I will try to look in the companion examples, good suggestion. The previous thread that was referenced also discussed how they couldn't find the formula as well.
And actually it is Blodgett's book with Lincoln Arc Welding Foundation from 1966.
And actually it is Blodgett's book with Lincoln Arc Welding Foundation from 1966.
The Nreq values are simply tabulated values in that table - they are driving the calculations for the allowable loads given in the rest of the table. That is, you determine the actual bearing length that you need (based on beam properties and loading). Then, you take that value and enter the design table to find the allowable capacity of a seated angle based on the bearing length required. The longer the required bearing length, the larger the eccentricity is on the projected angle leg, reducing the overall capacity of the connection.
If you are trying to determine the relationship of the Nreq to the outstanding leg strength reported in the table, it is as follows:
The seat angle is checked for shear and for bending of the horizontal angle leg to find the allowable load on it. As noted in the table, values above the solid black line are controlled by shear, values below are controlled by bending. Bending in the leg is found by multiplying the eccentricity of the bearing point times the shear load. Or, conversely, the allowable load can be found by dividing the max allowable bending moment on the angle leg by the eccentricity of the connection. The eccentricity is the clear space between the beam end and the back of the angle plus 1/2 the bearing length (Nreq) minus "k" of the angle (which is generally the angle leg thickness plus 3/8") See image below:
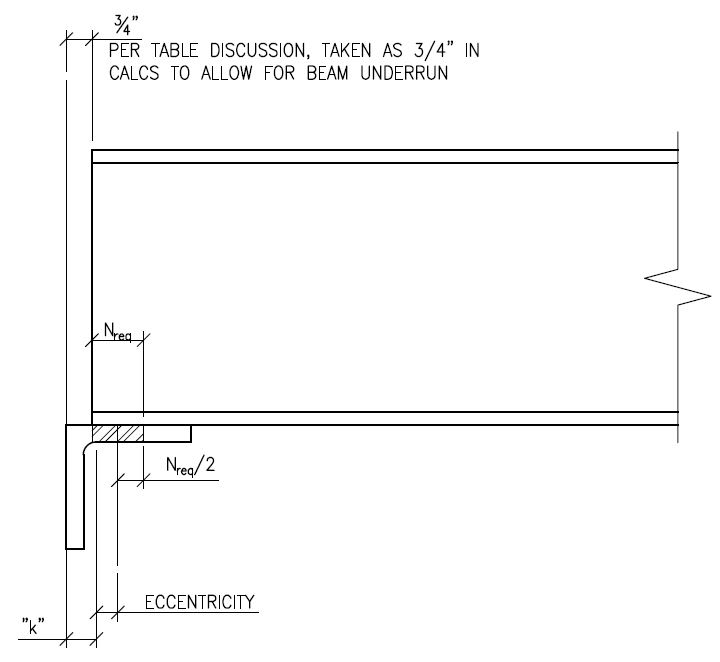
So, if we have a 3/8 by 6" long angle, we can calculate the allowable moment in the leg per spec section F11, Mn=Mp=FyZ. so 36ksi * 6in * 0.375^2 / 4 = 7.59 in-kip and phi*Mn = 0.9 * 7.59 = 6.831 in-kips
Then, lets say our required bearing area is 1", this would give an eccentricity of 3/4" + 1/2*1" - 3/4" = 0.5"
Finally, our allowable shear load would be phiMn/eccentricity = 6.831 in-kips / 0.5in = 13.66 kips. This corresponds to the 13.7 kip value shown in the table.
If you are trying to determine the relationship of the Nreq to the outstanding leg strength reported in the table, it is as follows:
The seat angle is checked for shear and for bending of the horizontal angle leg to find the allowable load on it. As noted in the table, values above the solid black line are controlled by shear, values below are controlled by bending. Bending in the leg is found by multiplying the eccentricity of the bearing point times the shear load. Or, conversely, the allowable load can be found by dividing the max allowable bending moment on the angle leg by the eccentricity of the connection. The eccentricity is the clear space between the beam end and the back of the angle plus 1/2 the bearing length (Nreq) minus "k" of the angle (which is generally the angle leg thickness plus 3/8") See image below:

So, if we have a 3/8 by 6" long angle, we can calculate the allowable moment in the leg per spec section F11, Mn=Mp=FyZ. so 36ksi * 6in * 0.375^2 / 4 = 7.59 in-kip and phi*Mn = 0.9 * 7.59 = 6.831 in-kips
Then, lets say our required bearing area is 1", this would give an eccentricity of 3/4" + 1/2*1" - 3/4" = 0.5"
Finally, our allowable shear load would be phiMn/eccentricity = 6.831 in-kips / 0.5in = 13.66 kips. This corresponds to the 13.7 kip value shown in the table.
ProgrammingPE
Structural
srm01 said:Page 5.2-2 equation (2): N = R/(t_w*(0.75*sigma_y))-K
This formula from Blodgett's Design of Welded Structures is outdated. The formula shown is the Web Local Yielding check rearranged to solve for N. The current formula is AISC 360-16, Equation J10-3 which when rearranged is:
N = Ω*R/(t_w*sigma_y) - 2.5*K
(Safety factor has changed and 2.5*K is used instead of just K) (Current formula uses lb instead of N and Fyw instead of sigma_y but I kept them the same here just to keep the discussion consistent).
Determining the Nreq value requires more than just this check, though. You also need to check Web Local Crippling, which comes from either Equation J10-5a or J10-5b. Nreq also cannot be less than K per Section J10.2 in the definition for lb.
Nreq will then be the largest of Nreq from Web Local Yielding, Nreq from Web Local Crippling, and K. You go into the Table 10-5 with this value in order to determine the Flexural Yielding and Shear Yielding capacity of the angle.
Structural Engineering Software: Structural Engineering Videos:
- Thread starter
- #7
- Status
- Not open for further replies.
Similar threads
- Locked
- Question
- Replies
- 8
- Views
- 2K
- Locked
- Question
- Replies
- 4
- Views
- 2K
- Locked
- Question
- Replies
- 5
- Views
- 2K
- Question
- Replies
- 1
- Views
- 2K
- Replies
- 2
- Views
- 8K
