Need Advice on Fluid System Flow Calc

[jchak65]

Hey everyone,

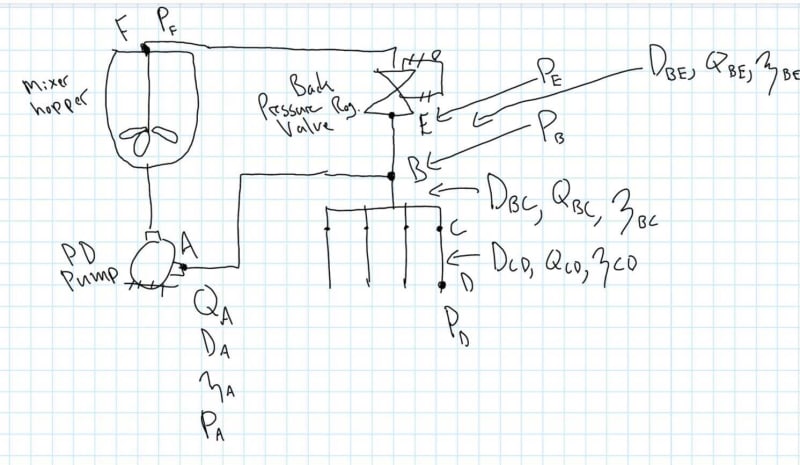
I have been working with this fluid system where we are pumping a thixotropic slurry with a positive displacement pump at a known flow rate (Qa) through a section of tubing up to a tee (B). The flow rates I see us working in yield a Re < 2300 so I am assuming we are laminar. At the tee we split to a discharge line (B-D) where we are pushing the slurry up against discharge which can accept a maximum flow rate if the necessary pressure is available to push the slurry through the volumetric flow control at D - I don't think we can say that D is at ambient pressure as slurry is pushed into a known volume, displacing the air through a loose seal, though maybe it is technically at ambient. The other branch of the tee goes up to a backpressure regulating valve where we add a set amount of backpressure to the lines to ensure our pressure at D is sufficient for the discharge we require - from testing I know what I need Pd to be, and from the pressure drop in the line I can figure out what additional backpressure we need to add in order to achieve this. After the backpressure regulating valve at E we return up to the hopper in a recirculation line E-F. So one side of the tee (B) dumps into the discharge (D) into a blocked

I have used the Power Law and am able to calculate the viscosity of the slurry at each diametrical/flow rate change in the system to help me then calculate the head pressure required to move that slurry through various sections of line at a set flow rate.

The question I'm running into is that we know the flow rate at A as we have a PD pump...I would like to just assume that we will be seeing our maximum/desired flow rate at D and that the rest of the flow will go up through the return line, however my calcs show that we will have a higher pressure drop from B-D than B-F due to the diameter change which we incur at C (shrink down significantly). Needless to say I can't say that we'll be seeing the maximum flow rate at D with the flow rate we are pushing at A. Again, I can calculate the viscosity at each point in the system, but I require the flow rate to do so as it is shear thinning. My current calc has me setting Qcd at my desired flow rate (the maximum which can be let through there), pushing the rest of Qa up through Qbe, and applying enough backpressure at the regulator to get Pd after the pressure drops from just the flow from Qcd...I just don't think I can assume these flow rates will be correct at the tee.

I haven't found a good method to determine how the flow rate will split at B in this scenario. I don't see a way to use Bernoulli's here, nor does poiseuille's law seem to have a place here.

I have seen mentions of "trial and error" (which sounds like a rough approach) where I can plot the flow rate vs pressure drop from B-F and do the same for B-D and find out at what flow rate they have the same pressure drop. If I do this approach then I suppose I would just add those flow rates and set that to be the flow rate from the pump, Qa? I'm just not seeing how that ties into me achieving the pressure Pd that I require, and how the backpressure regulating valve comes into the equation there.

Any thoughts on how I could proceed in determining what I need to set Qa to to achieve a desired Qcd and Pd in this scenario?

 

[1503-44]

Pipe flow is indeterminate, when you are not able to define 2 of the 3 primary variables, upstream pressure, downstream pressure, or flow rate.

If you assume a pressure at D1-D4, and presumably you know the suction pressure of the pump and the pump's differential pressure capability and flow rate, that is basically enough to solve for flows in each pipe in the system. Assume the backpressure valve is full open for the moment.

If D can be atmospheric, assume it is, at least for now.

You can work out the pressure at B by starting at pump discharge.

With pressure at B and D, work out the flow going through B-D.
Flow going to pump suction through the mixer Qb-a = Qa-b - Qb-d
Calculate the flow going through B-Asuction.
If it is not equal to Qa-b, Try making Qa-b = to the average of the two values and calculate the flow now going to B-D.
Keep doing that until flow into and away from B are equal and the pressure drops to pump suction and to D equal suction pressure and atmospheric pressure respectively.

At any time you can close the pressure control valve a little to increase the pressure drop from B to A to exactly set the pressure drop in B-A to precisely the value that you need to arrive at pump suction pressure. If you do that, then you have fixed the solution to leg B-A for that particular flow rate and you only have to solve the B-D leg.

I'm not entirely clear on what's going on at all the outlets D1-4 at point D.

 

[jchak65]

Hmm, I never considered using the suction of the pump in this calculation and did not think it would be necessary....The pump is capable of -12.3 psi suction, however we are positively feeding the pump with gravity and a vertical auger in the mixer. After the pump I would not think the suction side would come into affect as it is a positive displacement pump and pressures before the pressure side of the pump should not have an impact.

So yes, I have P_D, I know what Q_D would be (once we have the sufficient flow from A), I need to solve for Q_A and Q_BE and then can use that to solve for P_A and the rest of the pressures.

Would I simply use the following two equations to solve for these two unknowns:

Q_A=Q_BC+Q_BE

E_in=E_out
P_A+1/2*(density)*V_A²+(density)*g*h_A=[P_BC+1/2*(density)*V_BC²+(density)*g*h_BC]+[P_BE+1/2*(density)*V_BE²+(density)*g*h_BE]

I suppose I don't really have values for P_A, P_BC, or P_BE though...

 

[1503-44]

You do need to define, or be able to calculate the downstream pressure somewhere in B-A. A minimum suction pressure should be set at least to meet the pump's NPSHR. Otherwise define a pressure at the mixer inlet. You must know, or be able to calculate 2 of the 3 primary variables. Pin, Pout, or Q, You can calculate Pb, because you know Pa and Qa-b. You do not know Qb-a, so you have to set a downstream pressure somehow, somewhere in that leg, or you have to iterate Suction pressure and be able to control discharge pressure to the original value you assumed.

Yes, Qab = Qbe+Qbc
Qbe=Qef
Qef=Qfa
Qbc=Qcd
All the other pipes near D?, must have Q=0. I dont know what that fork looking thing is. Can you explain?

Bernoulli is not the equation to use. You need to select a pressure loss equation (as a function of the flow) for each pipe. I suggest for now you assume that you have water, use the Colebrooke White equation to find pressure drops in terms of pipe diameter, Velocity, Reynolds number and friction factor until you understand how this system flow analysis stuff works. Take an 6" diameter pipe 50ft long, an upstream pressure of 100 psig, water at 70°F. Assume a flow rate of 500 gpm and calculate the outlet pressure.

 

[jchak65]

The other pipes near D are all the same as D. They get the same flow rate as D, same pressure (well, close to it as the line lengths are slightly different), etc. I had already used Colebrook White and the Power Law to calculate pressure drop in all of the lines at set flow rates. I have used these calcs to calculate pressures at various points in the system, and drops across different sections.

I just realized a potential solution for this....let me know if this sounds like a reasonable approach:
-I am setting my flow rate at the leg of the tee going from B-C (Qb-c).
-At this flow rate I can calculate the pressure drop I'm seeing from B-D.
-If I then vary the flow rate from B-F until the pressure drop B-F equals that from B-D, I then can set the flow rate Qb-f at this value.
-With equal pressure drops through each leg I should now expect to see these flow rates through each leg (Qb-f and Qb-c).
-I can now simply get my pump to pump at the sum of these flow rates and add whatever backpressure needed to get the desired Pd, while still having the calculated flow rates Qb-f and Qb-c through each line.

Does this make sense?

 

[1503-44]

Oh. OK. Your equation post confused me, because it is not needed to solve network flows. I thought you were totally lost. We ignore Bernoulli effects for pressure drop determinations. You can consider those usually small effects later. Great.

In that case, D is 4 pipe discharges, calculate Qbc = Qd1 + Qd2 + Qd3 + Qd4 using P_D1-D4 = atmospheric, or 4 times the Qcd value you have now.

Getting close...
Yes. Calculate the flow in leg B-D using pressures Pb and Pd.
Calculate the flow in leg B-F using Pb and the mixer pressure Pf.
Sum those two flows. Assume that is the flow in pipe A-B.
Calculate the pressure drop in pipe A-B. Add that pressure drop to Pb to get the pressure at A.
Assume that is your pump discharge pressure.
Check if you can set the pump to deliver Qa = Qbd + Qbf at that assumed pump discharge pressure.
If you can, we can keep going. If not, then go back to "Getting close".

You can adjust the control valve to add or reduce pressure drop in that leg. That will change the legs flow rate, so you may/will have to recalculate its pressure drop and Pb and Qab, Pf, etc. if you change it a lot. If the new pressure drop is small, within your error tolerance, you might call it a solution and proceed.

Now you have to check the pump.
The pressure at the mixer -pressure loss between mixer and Pump suction must be greater than pump NPSHR. Now you must also check the pump differential pressure. If the pump can deliver Qab with a diff pressure of Pdischarge-Psuction and Pdischarge = Pa, that can be a solution.

If suction pressure was too low, you have to open the control valve a little and recalculate Pb & Qbf, Qab, Qbd, Qab as before. If suction pressure was too high, close the valve a little and recalculate all those same. Then check the valve. It should be able to be set to allow Qbf at some %open while keeping pressure drop in Qbf to hold your last suction pressure.

The ABEFA is a loop. Flow must always be constant in that loop, except for Qab, which must = Qbf + Qbd and the sum of pressure drops of pipes AB, BE, BF + control valve's pressure drop must be equal to the pump differential pressure. If not, basically make a slightly different assumption for pump discharge pressure or the leg's flow rate and recalculate everything again. Calculate Qbd, using the latest Pb and atmospheric pressure and it should equal Qab-Qbf. If it does, or is close enough, its done.

You know when your finished when flows in/out at each junction add up to zero, pressure drop in pipes ABEFA plus the pressure drop at the control valve add up to pump differential pressure, or are algebracially zero. (Pdiff at the pump is a "positive pressure drop") Qab = Qbf+Qbd and Pb-Pd = atmospheric pressure.

 

[LittleInch]

jcjack65,

You seem to me making this a whole heap more complex that it should be as far as I can see.

A PD pump as you say pumps more or less a fixed volumetric flow rate regardless of the pressure it puts out (Pa). Now the line isn't truly vertical on a flow to pressure graph, but it's usually pretty close. Also because Pa is in theory unlimited, the normal result is that either a relief valve is installed or if the pressure goes too high then the motor or driving device may eventually stall if you stop flow.

So for the flow side you simply need to sum your total flows you want along your four lines and then add a little bit ( say 10%) for the flow return line.

Pressure control at the tee B is now in your control by determining how much flow resistance you add to the return line. There will be some sort of minimum pressure at B which is the frictional pressure of the line from B to F plus pressure in the vessel. This will be when your flow control valve is full open.

Then as you close your valve the pressure will start to rise because the pump is pumping the same volume, but now some it needs to go somewhere else or result in increased pressure to flow the same amount back down the return line. Always remember that the pressure at a junction or node has to be the same regardless of where the flow goes from that node or junction and conservation of mass - mass in = mass out in a steady state flow situation.

You appear to know what you want say Qd to be, you know the frictional drop B to D at that flowrate and velocity, so you know what pressure you need at Pb.

For the pump just add on the pressure drop in A to B, subtract Pf and make that your rated discharge pressure( I would add a bit here). you know what flow you want from above.

What's more to find out?

Remember - More details = better answers
Also: If you get a response it's polite to respond to it.

 

[pierreick]

Hi ,
Attached a excel sheet for hydraulic calculation of systems ( 2exemples),including equations .
Make sure you have sufficient enough input data to solve your system.
Hoppe this is going to help you .
Pierre