Masonry Shear Wall Flanges 2

[DCBII]

I'm doing low-rise masonry shear walls in seismic design category D. There are several piers in each line of resistance, and some of them have flanges due to intersecting walls. What's the industry doing out there to account for the flanges? Do you place joints to isolate intersecting walls from each other to simplify the analysis? The strain-compatibility analysis to determine the wall's flexural strength and level of ductility is intensive. The code requires flanges be considered, since they drive up the flexural strength, which is what the required shear strength is based on. Maybe I'm wrong, but I get the impression most engineers ignore them, which is unconservative.

 

[MrHershey]

Should technically consider the full section with en effective flange width for developing shear. Think ACI 530 will let you out of it if you provide movement joints between wall and flange but that's a little dubious in my opinion if you've got a stiff diaphragm (like a concrete slab).

You'll have to count the rebar in the effective flange width for tension but fortunately compression flange typically doesn't move neutral axis around much. Effective flange for tension is based on wall height, so fortunately shouldn't have a huge effect for low-rise assuming your walls aren't packed with reinforcement (this could be why you get the impression most engineers ignore them).

NEHRP has a guide that provides some guidance for this: Link (PDF)

Excerpt:
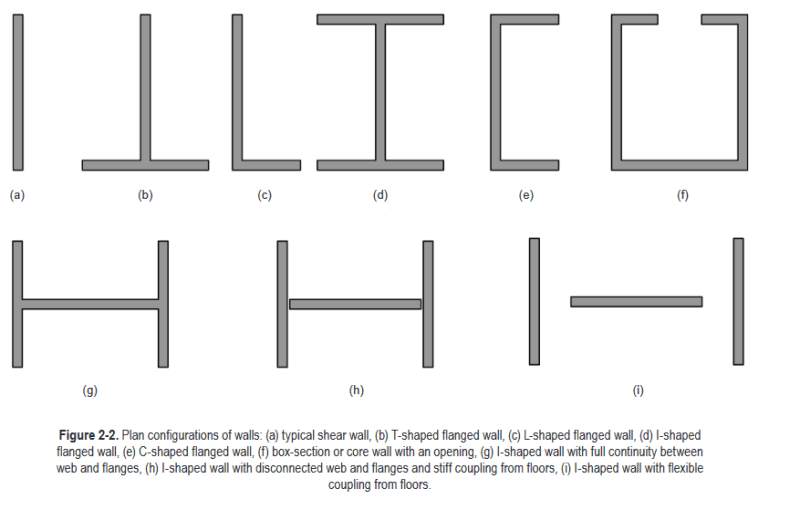
Most reinforced masonry codes and design guides provide rules for the design of simple, planar wall elements as in Figure 2-2(a), but in practice such walls can be part of complex structural elements and systems that affect their behavior, as illustrated in Figures 2-2(b) through 2-2(f). The designer can choose to design and detail such walls to have an integral cross section, with the wall segment aligned parallel to the lateral shear force acting as web and the perpendicular wall segments acting as tension or compression flanges as in Figure 2-2(g). Alternatively, the designer can choose to treat groups of intersecting walls as individual planar elements, provided that they are sufficiently separated so that shear cannot be transferred between them either through the masonry or through stiff horizontal diaphragms. Depending on the nature of the diaphragm, small gaps between wall segments as in Figure 2-2(h) may not be sufficient to decouple the walls, and some separation may be required as in Figure 2-2(i).

 

[MrHershey]

Oh, also technically developing the flexural capacity of the wall (plus effective flanges) in shear is only required for strength (LRFD) design of special walls.

ASD applies a 50% increase to all in-plane shears due to seismic in special walls to try and mimic this, but there's no requirement to develop the flexural capacity of the wall.

Most engineers still do ASD, so there's another reason it may seem like the flanges are getting ignored.

Code section is 1.18.3.2.6.1 in ACI 530-11.

 

[DCBII]

Thanks for your response MrHershey. The lack of other responses to this question is concerning. It makes me think we as a profession are sweeping something under the rug.

Even for ASD, you still have to make sure you do not exceed the balanced reinforcement ratio for a special shear wall. All those extra bars in a flange can add up and push you over the edge into a masonry crushing failure mode. Add all the extra shear ties you want, and a 50% increase to the shear load, but if you're trying to get a plastic hinge to form you can't exceed the balanced ratio. Otherwise the wall will fail in a non-ductile flexural mode, and it will behave more like an ordinary shear wall.

The unbalanced ratio is a nightmare to calculate. It's influenced by bar arrangement, axial load, and flanges, and it's an iterative calculation. I think most engineers are just saying "that's too complicated" and skipping the crucial part of the design that controls the ductility. The common practice I've seen is that engineers add "hold-down" reinforcement at the ends of the walls, but to me this just makes the wall less ductile by potentially over-reinforcing it for flexure. Beyond the first bar placed, every additional vertical bar in the wall makes it less ductile (even though it adds capacity) by decreasing the strain in the extreme tension steel, especially bars added near the ends.

There will also be a stiffness change to the piers with flanges. Flanges increase the moment of inertia very quickly. Any piers with flanges will draw more load to them.

 

[DCBII]

After spending hours playing with calculations and digging through the NEHRP design guide, I've found some solid answers to my question. I'll post them here for future reference for others.

NEHRP recognizes that some walls will be shear-dominated no matter what you do. In such cases, an R value of 5 per ASCE 7 is not justifiable. NEHRP recommends using an R of 1.5 when shear-dominated behavior is expected. Most low-rise construction falls into this category. R of 1.5 is essentially elastic behavior. The effect of the flanges on the wall ductility becomes a moot point, although they still do affect stiffness and load distribution.

Quoting the NEHRP Design Guide:

Design of Shear-dominated Walls

It is the implicit intent of ASCE 7 and TMS 402 that special walls be fexure-dominated, with behavior that justifes the response modifcation factor R=5 assigned to them. However, as discussed in Section 3, walls designed in accordance with the provisions of these codes may still be shear-dominated. There is little direct guidance in TMS 402 to address this situation, which raises concerns that require the engineering judgment of the designer. The frst is the possibility of brittle shear failure in elements of the gravity load bearing system, albeit at lateral loads that may be much higher than the code-required design loads. This Guide does not address the complexity or repercussions of this possibility, nor does it advocate one approach or another to address it, because too many scenarios are possible.

Another implication of shear-dominated behavior in wall elements is the understanding that such elements may behave nearly elastically, attracting forces much higher than those calculated using a response modification factor R=5. This has implications for both the wall element itself and for other elements of the seismic load path that will have correspondingly increased demand. Such elements may include diaphragms, diaphragm chords, connections of diaphragms to shear walls, and collectors.

One approach available to the designer would be to design all elements of the seismic lateral load- resisting system associated with shear-dominated walls using a response modifcation factor less than the code value for special reinforced masonry walls (for example, R =1.5).

And again, in Section 3 of the design guide:

The implicit goal of TMS 402 is that special masonry shear walls be fexure-dominated and ductile. The code indirectly encourages designs that meet this goal through prescriptive requirements for distribution of reinforcement, limitations on bar diameters, maximum reinforcement restrictions, and other provisions, but these requirements may not be suffcient to produce ductile behavior. When a special shear wall has a shear-span-to-depth ratio Mu/(Vudv) greater than one with a well-designed plastic hinge zone (Paulay and Priestley 1992), these requirements plus the required capacity-based design for shear generally result in fexure-dominated, ductile behavior. However, when a special shear wall has a shear-span-to-depth ratio less than one or a high axial load, the same combination of prescriptive requirements may still result in a wall that is shear-dominated and brittle. This is often the case for low-rise masonry buildings, which constitute most masonry construction in the United States.

 

[MrHershey]

Perhaps picking nits here, but I'd stop short of saying NEHRP 'recommends' using an R of 1.5. That's an example and you're certainly welcome to follow it, but I don't think I'd buy that this is the approach NEHRP recommends using. They pretty explicitly avoid recommending anything: 'This guide does not address the complexity or repercussions of this possibility, nor does it advocate one approach or another to address it'.

 

[DCBII]

You're right: "recommends" is the wrong word. They fall short of proposing any other alternatives to this approach though. They've identified a problem where the codes don't match reality, and offered one potential solution. It seems like a sensible approach... better than pretending I have a ductile system because I've met a few prescriptive requirements, and then taking an 80% reduction (R=5) in my seismic forces based on that assumption.

 

[KootK]

Thanks very much for reporting back on this DCBII. I'd thought I'd responded but apparently did not. I was going to give a similar response. Namely, that I almost never encounter a masonry shear wall system that I would expect to be governed by flexural response. They're generally squat and dominated by shear behavior in which case the question of flanges becomes pretty irrelevant. Or, I suppose, it's hyper relevant in that they clearly should not be envisioned as flanges in the flexural sense.

It seems to me that this is NEHRP's recommendation irrespective of any goofy disclaimers their lawyers may have foisted upon them. They've made it pretty clear what they think the issue is and how it should be addressed by a qualified designer. I don't base my work on the assumption that I'll eventually find myself in court but, if I did find myself in court, I'd love to trot out the NEHRP stuff and suggest that I'm on the right side of modern industry thinking, even if the final decision rests with me. And I'd loathe to be in the opposite position.

I like to debate structural engineering theory -- a lot. If I challenge you on something, know that I'm doing so because I respect your opinion enough to either change it or adopt it.