Navigation
Install the app
How to install the app on iOS
Follow along with the video below to see how to install our site as a web app on your home screen.
Note: This feature may not be available in some browsers.
More options
Style variation
-
Congratulations TugboatEng on being selected by the Eng-Tips community for having the most helpful posts in the forums last week. Way to Go!
You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Location and orientation 2 1
- Thread starter Sa-Ro
- Start date
- Status
- Not open for further replies.
Hi All,
As usual, I agree with pmarc. If the feature was an arc-shaped or other curved surface, then the orientation control could not be achieved without using composite profile.
It's easy to show that the committee intended to apply composite profile to a single feature - the first example in the Composite Profile is literally titled and described that way. Unfortunately, the "feature" that they chose isn't really a single feature ;^/. It's a pattern, whose tolerance zones are grouped by the all-around symbol, which is a grouping mechanism but wasn't described as such until 2018. But that's a whole other story.
I don't see any reason why composite profile cannot be applied to a single planar surface. If we were to do that, the meaning would be clear. But I would agree that it should not be, because the combination of a profile tolerance and an orientation tolerance would be more straightforward to understand.
Evan Janeshewski
Axymetrix Quality Engineering Inc.
As usual, I agree with pmarc. If the feature was an arc-shaped or other curved surface, then the orientation control could not be achieved without using composite profile.
It's easy to show that the committee intended to apply composite profile to a single feature - the first example in the Composite Profile is literally titled and described that way. Unfortunately, the "feature" that they chose isn't really a single feature ;^/. It's a pattern, whose tolerance zones are grouped by the all-around symbol, which is a grouping mechanism but wasn't described as such until 2018. But that's a whole other story.
I don't see any reason why composite profile cannot be applied to a single planar surface. If we were to do that, the meaning would be clear. But I would agree that it should not be, because the combination of a profile tolerance and an orientation tolerance would be more straightforward to understand.
Evan Janeshewski
Axymetrix Quality Engineering Inc.
Burunduk
Mechanical
- May 2, 2019
- 2,580
pmarc said:But what if the toleranced surface was an arc or something?
axym said:If the feature was an arc-shaped or other curved surface, then the orientation control could not be achieved without using composite profile.
Option 1:
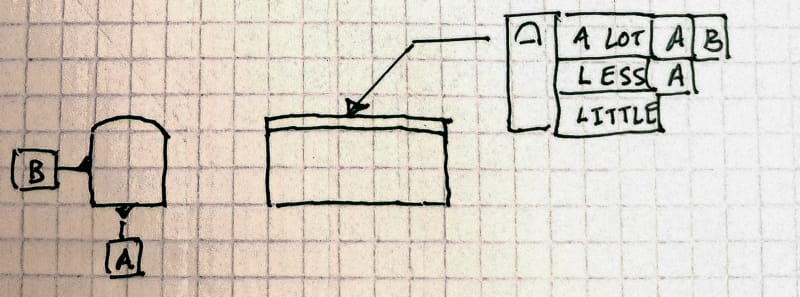
Option 2:
Burunduk
Mechanical
- May 2, 2019
- 2,580
Because there is no form control by parallelism of each line element as opposed to profile wrt A in the middle segment?
I agree, but the form ends up being controlled to a tighter tolerance in both options (by cylindricity or the last segment of composite), and thus profile in the middle segment effectively only controls orientation so what's the difference at the end result?
Or did you mean something else?
I agree, but the form ends up being controlled to a tighter tolerance in both options (by cylindricity or the last segment of composite), and thus profile in the middle segment effectively only controls orientation so what's the difference at the end result?
Or did you mean something else?
Burunduk,
I think what pmarc means is that controlling the parallelism of the line elements only controls the orientation in one "sense". It wouldn't control the orientation of the surface in the view that the cylindricity callout is in.
Evan Janeshewski
Axymetrix Quality Engineering Inc.
I think what pmarc means is that controlling the parallelism of the line elements only controls the orientation in one "sense". It wouldn't control the orientation of the surface in the view that the cylindricity callout is in.
Evan Janeshewski
Axymetrix Quality Engineering Inc.
Burunduk
Mechanical
- May 2, 2019
- 2,580
axym,
The cylindrical surface has no orientation relationship in the usual sense with datum A in the view where the cylindricity callout is, or in the corresponding view for the composite case. It can only appear oriented in a certain way depending on where the top peak (or the theoretical axis if we are talking about the theoretical geometry) is located relative to datum B in conjunction with the width in this view.
It works OK with only datum feature A referenced for the orientation refinement in the second segment of composite because the orientation tolerance is floating within the location tolerance so the way the feature "looks" oriented in the view where it looks as an arc is limited by the upper segment that references B. But this "orientation" is not achieved by the second segment of the composite control anyway. This trait is location dependent.
To clarify further: suppose that all basic dimensions should be queried from the CAD model. The way the feature looks oriented in the view where its curvature is visible depends on the ratio between the basic distance of its axis from datum B and the width between the vertical faces in that view. However, this basic distance does not apply to the second segment of the composite profile. It wouldn't apply if datum feature B reference was repeated in the second segment, either.
The cylindrical surface has no orientation relationship in the usual sense with datum A in the view where the cylindricity callout is, or in the corresponding view for the composite case. It can only appear oriented in a certain way depending on where the top peak (or the theoretical axis if we are talking about the theoretical geometry) is located relative to datum B in conjunction with the width in this view.
It works OK with only datum feature A referenced for the orientation refinement in the second segment of composite because the orientation tolerance is floating within the location tolerance so the way the feature "looks" oriented in the view where it looks as an arc is limited by the upper segment that references B. But this "orientation" is not achieved by the second segment of the composite control anyway. This trait is location dependent.
To clarify further: suppose that all basic dimensions should be queried from the CAD model. The way the feature looks oriented in the view where its curvature is visible depends on the ratio between the basic distance of its axis from datum B and the width between the vertical faces in that view. However, this basic distance does not apply to the second segment of the composite profile. It wouldn't apply if datum feature B reference was repeated in the second segment, either.
mfgenggear
Aerospace
hey guys don't mean to jumping the middle of this.
as I not as knowable as some here.
intent is as follow.
flatness is used to have perfect contact with the mating part, better surface contact.
parallel is use when mounted in the assembly is still square. the two surfaces are not causing angularity errors.
I think the authors use of profile is a poor choice. and the OAL should be to a tolerance.
thus the experts are not agreeing how the poor guy on floor suppose to know.
but yes it gives the over all length tolerance.
flatness is verified to itself, to verify it, it must be on three points, then an indicator verified 3 places min. must be .12 MM flat.
parallel, the datum -A- is placed on a surface place and an indicator is run over the opposite surface.
and must be parallel. must be in tolerance with in .5 MM
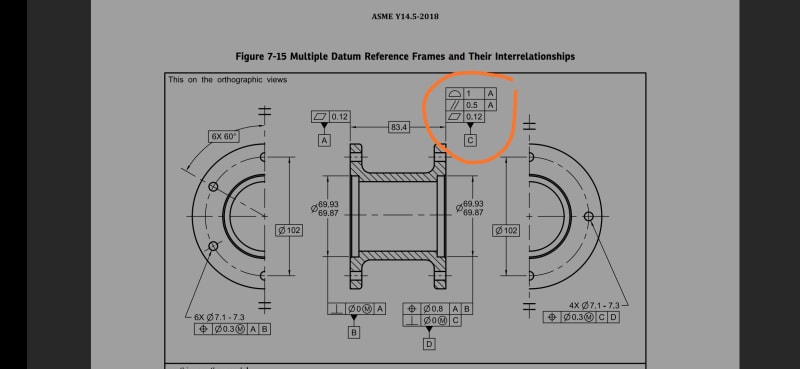
profile again the datum -A- is place on surface plate a height gage with an indicator is set by gage blocks to 83.4 ,
then it verified 3 places min and it has to be with in 1 MM. easy .
three separate verifications. now a days a CMM can do it all..
as I not as knowable as some here.
intent is as follow.
flatness is used to have perfect contact with the mating part, better surface contact.
parallel is use when mounted in the assembly is still square. the two surfaces are not causing angularity errors.
I think the authors use of profile is a poor choice. and the OAL should be to a tolerance.
thus the experts are not agreeing how the poor guy on floor suppose to know.
but yes it gives the over all length tolerance.
flatness is verified to itself, to verify it, it must be on three points, then an indicator verified 3 places min. must be .12 MM flat.
parallel, the datum -A- is placed on a surface place and an indicator is run over the opposite surface.
and must be parallel. must be in tolerance with in .5 MM
profile again the datum -A- is place on surface plate a height gage with an indicator is set by gage blocks to 83.4 ,
then it verified 3 places min and it has to be with in 1 MM. easy .
three separate verifications. now a days a CMM can do it all..
pmarc
Mechanical
- Sep 2, 2008
- 3,248
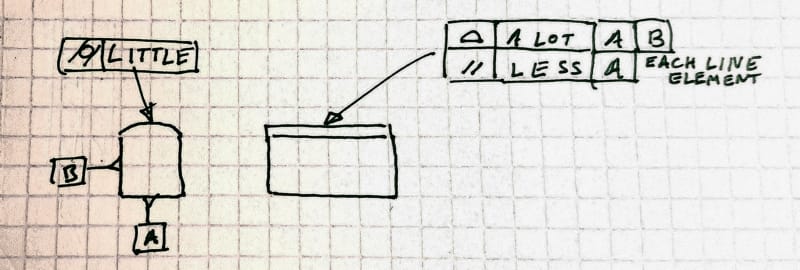
What I rather meant was that if we assume that the 2D tolerance zones defined by each line element parallelism callout lie in the planes parallel to the plane of the right view (which is debatable assumption, I agree), the tolerance value in that callout would have to be different in each cross section to produce a tolerance zone equivalent to the one created by the profile tolerance.
Burunduk
Mechanical
- May 2, 2019
- 2,580
pmarc,
I agree. I think that the 2D two-offset-lines tolerance zones for each line element parallelism would have to be on planes normal to datum A, not normal to the true profile of the arc (unlike in the case of profile of a line for example).
Would you also say that datum B should be referenced by the parallelism of each line element, to set a fully defined DRF-related orientation of these 2D planes and avoid problematic view-dependency?
So I agree that the two schemes are not equivalent in the sense that identical tolerance values for the second segment of the composite profile and parallelism of each line element would lead to different levels of orientation control. If identical tolerance values for "LESS" are assigned, the allowed variation would be equal in both schemes only at the line element that is at the top peak of the arc.
However, I don't think it would be much of an issue for the designer to assign the appropriate tolerance value that will satisfy the function, correspondingly to the tolerancing scheme of choice. Even though I made up that part I don't have an idea what the function is. The part looks like a loaf of bread. If it is indeed a loaf of bread, the orientation of the curved top relative to the base of the loaf can have a sloppy tolerance value which will not make a big difference if assigned either as part of a composite profile control or as part of the parallelism of each line element FCF in the second option. The baker will find it equally manufacturable anyway.
I agree. I think that the 2D two-offset-lines tolerance zones for each line element parallelism would have to be on planes normal to datum A, not normal to the true profile of the arc (unlike in the case of profile of a line for example).
Would you also say that datum B should be referenced by the parallelism of each line element, to set a fully defined DRF-related orientation of these 2D planes and avoid problematic view-dependency?
So I agree that the two schemes are not equivalent in the sense that identical tolerance values for the second segment of the composite profile and parallelism of each line element would lead to different levels of orientation control. If identical tolerance values for "LESS" are assigned, the allowed variation would be equal in both schemes only at the line element that is at the top peak of the arc.
However, I don't think it would be much of an issue for the designer to assign the appropriate tolerance value that will satisfy the function, correspondingly to the tolerancing scheme of choice. Even though I made up that part I don't have an idea what the function is. The part looks like a loaf of bread. If it is indeed a loaf of bread, the orientation of the curved top relative to the base of the loaf can have a sloppy tolerance value which will not make a big difference if assigned either as part of a composite profile control or as part of the parallelism of each line element FCF in the second option. The baker will find it equally manufacturable anyway.
So I agree that the two schemes are not equivalent in the sense that identical tolerance values for the second segment of the composite profile and parallelism of each line element would lead to different levels of orientation control.
It would also impose different levels of form control.
pmarc,
Sorry to put words in your mouth. I believe that you were thinking of the effect on the left, and I was thinking of the effect on the right:
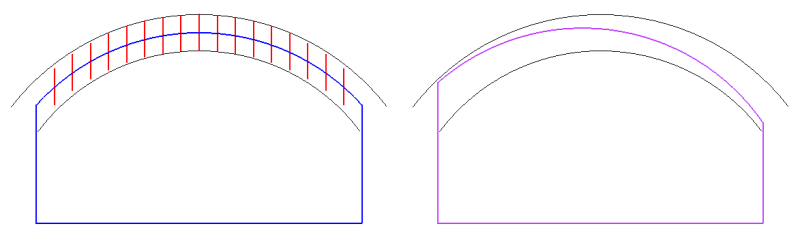
As the slope of the basic surface increases, the line element parallelism zones are not as vertically "tall" as the profile zone. I agree that this would happen.
I was thinking that the 2D parallelism zones would not control the "tilt" of the surface in the perpendicular direction, so that the surface could be tall on one side and short on the other, within the profile tolerance.
burunduk,
I imagine that you are thinking that the surface in the right-hand diagram could have resulted from translation, and would thus be allowed by the composite profile tolerance. This may be true, but I would say that this only occurs because the true profile has special case geometry (arc of a cylinder, with constant curvature). If the surface was not a simple cylindrical arc, but was a more general curve, then I don't think that the rotation could be duplicated by translation.
Evan Janeshewski
Axymetrix Quality Engineering Inc.
Sorry to put words in your mouth. I believe that you were thinking of the effect on the left, and I was thinking of the effect on the right:

As the slope of the basic surface increases, the line element parallelism zones are not as vertically "tall" as the profile zone. I agree that this would happen.
I was thinking that the 2D parallelism zones would not control the "tilt" of the surface in the perpendicular direction, so that the surface could be tall on one side and short on the other, within the profile tolerance.
burunduk,
I imagine that you are thinking that the surface in the right-hand diagram could have resulted from translation, and would thus be allowed by the composite profile tolerance. This may be true, but I would say that this only occurs because the true profile has special case geometry (arc of a cylinder, with constant curvature). If the surface was not a simple cylindrical arc, but was a more general curve, then I don't think that the rotation could be duplicated by translation.
Evan Janeshewski
Axymetrix Quality Engineering Inc.
Burunduk
Mechanical
- May 2, 2019
- 2,580
axym,
I was specifically addressing a simple cylindrical surface arc. I agree regarding other curved surfaces, but:
The so-called "orientation" of an arc in the view where its curvature is visible relative to a datum plane parallel to the axis of the theoretical geometry is not able to be "duplicated by translation", it can only be caused by translation.
Consider a modified figure of that part where the side surfaces are initially tangent to the arc at both sides as the graphic below attempts to show.
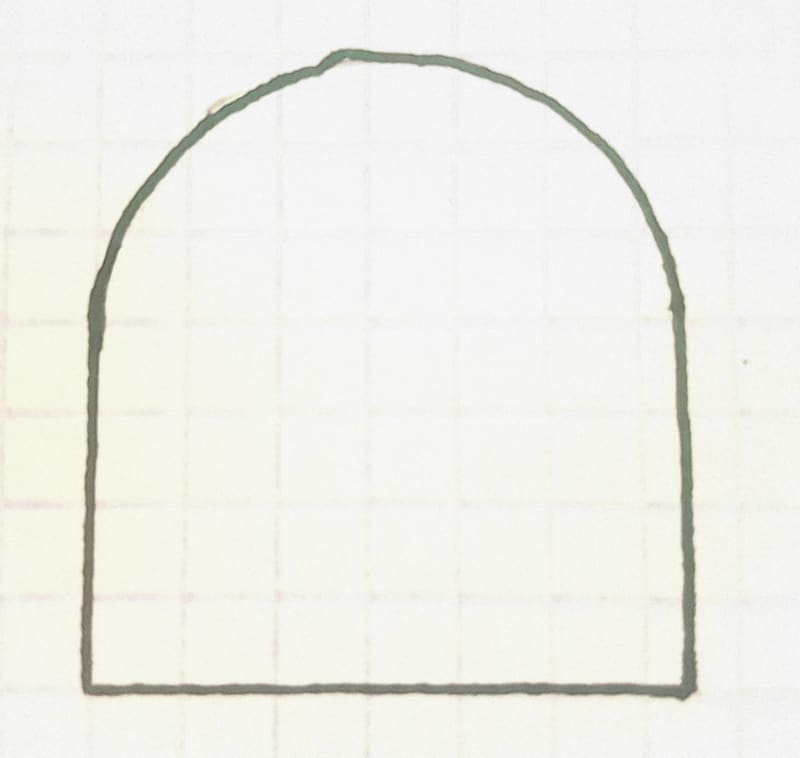
There is clearly no orientation relationship between the arc and the datum derived from the bottom surface: as long as there is tangency at both sides and assuming that the two vertical side faces are parallel and vertical, the imaginary line (2D description for clarity) that could connect the tangency points can only be horizontal. You are unable to rotate the arc to appear inclined. There is as much "orientation" relationship as there would be between a full cylinder and a plane parallel to its axis, at the rotational DOF about the direction of the axis of that cylinder.
Now consider that the tangency is canceled and the vertical side faces are adjusted to create corners where they connect with the arc - this could be achieved by removal of material from both sides. The new side faces are shown dashed:
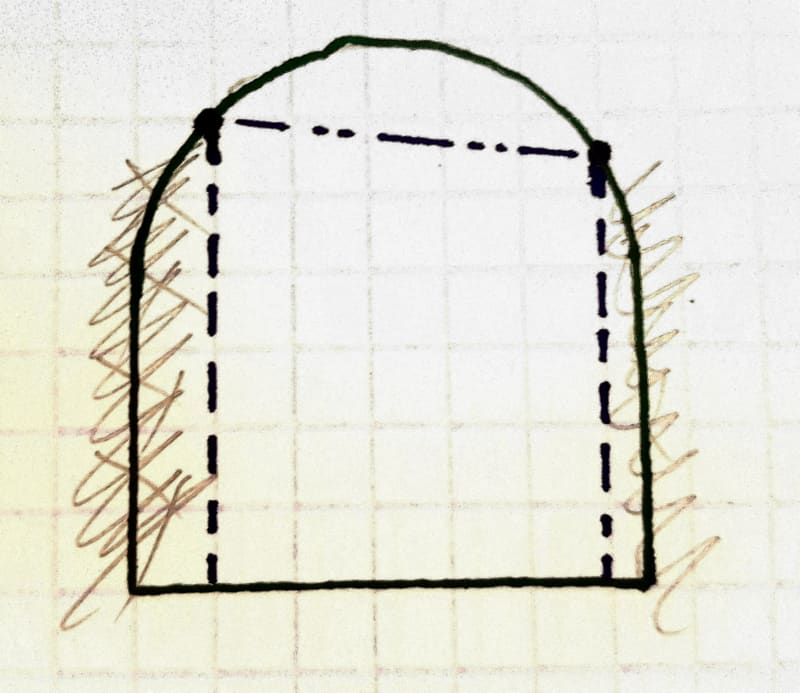
All of a sudden the arc looks like it could have all sorts of orientations, one of which is shown. That already looks fishy because the relationship between the arc and the datum derived from the bottom face didn't change, it is only the side faces that were modified. We can ignore that fishiness but only until we try to analyze the difference between the original condition of tangency and the modified version: the axis of the theoretical arc was initially centered to the center plane between the vertical sides. In the modified version, it is no longer centered. If it is so, what looks like an "inclination" is actually translation of the axis of the theoretical arc relative to the center of the width.
chez311,
I don't think that parallelism of each line element controls form at all. The feature could be produced not arc-shaped and still conform to the parallelism of line elements requirement. In this scheme, only the cylindricity requirement is the final word regarding form. The profile FCF could control the form if it wasn't for the cylindricity tolerance. The composite tolerance is not much different in the sense that only the last datum-less segment is the final word regarding form. The insignificant difference is that in the composite profile case, each segment could control form if there were no subsequent segments. But that is only a hypothetical analysis that doesn't affect the end result - the form is controlled with the "LITTLE" tolerance value in both options.
I was specifically addressing a simple cylindrical surface arc. I agree regarding other curved surfaces, but:
The so-called "orientation" of an arc in the view where its curvature is visible relative to a datum plane parallel to the axis of the theoretical geometry is not able to be "duplicated by translation", it can only be caused by translation.
Consider a modified figure of that part where the side surfaces are initially tangent to the arc at both sides as the graphic below attempts to show.

There is clearly no orientation relationship between the arc and the datum derived from the bottom surface: as long as there is tangency at both sides and assuming that the two vertical side faces are parallel and vertical, the imaginary line (2D description for clarity) that could connect the tangency points can only be horizontal. You are unable to rotate the arc to appear inclined. There is as much "orientation" relationship as there would be between a full cylinder and a plane parallel to its axis, at the rotational DOF about the direction of the axis of that cylinder.
Now consider that the tangency is canceled and the vertical side faces are adjusted to create corners where they connect with the arc - this could be achieved by removal of material from both sides. The new side faces are shown dashed:

All of a sudden the arc looks like it could have all sorts of orientations, one of which is shown. That already looks fishy because the relationship between the arc and the datum derived from the bottom face didn't change, it is only the side faces that were modified. We can ignore that fishiness but only until we try to analyze the difference between the original condition of tangency and the modified version: the axis of the theoretical arc was initially centered to the center plane between the vertical sides. In the modified version, it is no longer centered. If it is so, what looks like an "inclination" is actually translation of the axis of the theoretical arc relative to the center of the width.
chez311,
chez311 said:It would also impose different levels of form control.
I don't think that parallelism of each line element controls form at all. The feature could be produced not arc-shaped and still conform to the parallelism of line elements requirement. In this scheme, only the cylindricity requirement is the final word regarding form. The profile FCF could control the form if it wasn't for the cylindricity tolerance. The composite tolerance is not much different in the sense that only the last datum-less segment is the final word regarding form. The insignificant difference is that in the composite profile case, each segment could control form if there were no subsequent segments. But that is only a hypothetical analysis that doesn't affect the end result - the form is controlled with the "LITTLE" tolerance value in both options.
Burunduk,
Wow, I had never thought through the arc orientation issue that far. I have learned over the years that many concepts are better illustrated using general-case surfaces, because special-case geometry often has unique properties such as the one you've described.
Evan Janeshewski
Axymetrix Quality Engineering Inc.
Wow, I had never thought through the arc orientation issue that far. I have learned over the years that many concepts are better illustrated using general-case surfaces, because special-case geometry often has unique properties such as the one you've described.
Evan Janeshewski
Axymetrix Quality Engineering Inc.
Burunduk
Mechanical
- May 2, 2019
- 2,580
axym,
If the concept is illustrated using general-case surfaces, caution should be taken to make sure that what is true for the general-case surface such as non-cylindrical curve is not deduced to all shapes that have common traits with it such as a cylindrical arc. I would even say that it is better to avoid such generalizations and it is necessary to clarify the specific relationships that features can have with each other in the different degrees of freedom as derived from the nominal geometry.
For example, it is pretty obvious that two perpendicular planar surfaces don't have a location relationship to each other. It is also easy to see that two parallel surfaces have both a location and orientation relationship with each other, and that relationship is clear and valid regardless of any other features of the part.
But, there are cases that are less trivial: if a horizontal face initially parallel to a bottom face is modified to have some inclination, there is no longer an independent location relationship between these features. The height of the inclined surface depends on the location of the vertical side faces relative to the theoretical intersection between the inclined top face and the bottom face, and the width between the vertical faces. In other words, there is no location relationship between two planar surfaces that are at a non-zero angle to each other, and I don't know how many people realize that.
So, just as the exclusively mutual orientation relationship between two nominally parallel planar surfaces can't be deduced to a planar surface and an arc, the exclusively mutual location relationship between two parallel planar surfaces can't be deduced to a planar surface and another planar surface at some nominal inclination to it. Consideration must be given to the effect of other features of the part on the required geometry.
When such relationships are specified by basic dimensions and geometrical controls, the designer must know how to specify the datum reference frame to involve all the relevant features. This is why I think that however does dimensioning and tolerancing training should address these things early in the process, even before degrees of freedom and the meaning of geometric characteristic symbols are explained.
If the concept is illustrated using general-case surfaces, caution should be taken to make sure that what is true for the general-case surface such as non-cylindrical curve is not deduced to all shapes that have common traits with it such as a cylindrical arc. I would even say that it is better to avoid such generalizations and it is necessary to clarify the specific relationships that features can have with each other in the different degrees of freedom as derived from the nominal geometry.
For example, it is pretty obvious that two perpendicular planar surfaces don't have a location relationship to each other. It is also easy to see that two parallel surfaces have both a location and orientation relationship with each other, and that relationship is clear and valid regardless of any other features of the part.
But, there are cases that are less trivial: if a horizontal face initially parallel to a bottom face is modified to have some inclination, there is no longer an independent location relationship between these features. The height of the inclined surface depends on the location of the vertical side faces relative to the theoretical intersection between the inclined top face and the bottom face, and the width between the vertical faces. In other words, there is no location relationship between two planar surfaces that are at a non-zero angle to each other, and I don't know how many people realize that.
So, just as the exclusively mutual orientation relationship between two nominally parallel planar surfaces can't be deduced to a planar surface and an arc, the exclusively mutual location relationship between two parallel planar surfaces can't be deduced to a planar surface and another planar surface at some nominal inclination to it. Consideration must be given to the effect of other features of the part on the required geometry.
When such relationships are specified by basic dimensions and geometrical controls, the designer must know how to specify the datum reference frame to involve all the relevant features. This is why I think that however does dimensioning and tolerancing training should address these things early in the process, even before degrees of freedom and the meaning of geometric characteristic symbols are explained.
pmarc
Mechanical
- Sep 2, 2008
- 3,248
Burunduk said:Would you also say that datum B should be referenced by the parallelism of each line element, to set a fully defined DRF-related orientation of these 2D planes and avoid problematic view-dependency?
Sorry for the late reply... Yes, this is what I would say.
Burunduk
Mechanical
- May 2, 2019
- 2,580
pmarc said:Sorry for the late reply... Yes, this is what I would say.
Thanks for your input on this.
- Status
- Not open for further replies.
Similar threads
- Locked
- Question
- Replies
- 6
- Views
- 879
- Locked
- Question
- Replies
- 38
- Views
- 2K
- Question
- Replies
- 6
- Views
- 10K
- Locked
- Question
- Replies
- 19
- Views
- 989
- Question
- Replies
- 9
- Views
- 14K