struggle67
Structural
- Mar 29, 2013
- 116
Hi,
I have a very slender precast beam. And I have to check lateral instability (LTB). I know how to account for it in a steel beam design according to EC3 but I do not know how to account for it in a very slender reinforced concrete beam. I couldn't find any guideline in EC2. The screenshot below is from EC2 and that's all I could find.

I am thinking to use this concept below which we normally use to calculate lateral restraint force required to prevent LTB for steel beams and get the equivalent lateral load. I will multiply that lateral force with an eccentricity (distance from C.A of the beam to the top compression face)to get the torsion. Then I will just either design the beam for that torsion or provide lateral restraint. May I know if my approach is logical & correct or is there any other way to do it? Thanks in advance for your help.
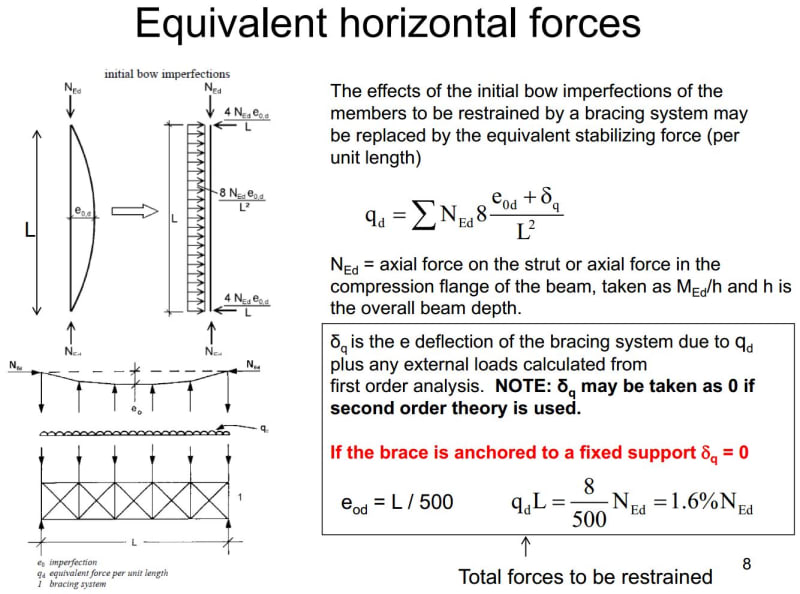
I have a very slender precast beam. And I have to check lateral instability (LTB). I know how to account for it in a steel beam design according to EC3 but I do not know how to account for it in a very slender reinforced concrete beam. I couldn't find any guideline in EC2. The screenshot below is from EC2 and that's all I could find.

I am thinking to use this concept below which we normally use to calculate lateral restraint force required to prevent LTB for steel beams and get the equivalent lateral load. I will multiply that lateral force with an eccentricity (distance from C.A of the beam to the top compression face)to get the torsion. Then I will just either design the beam for that torsion or provide lateral restraint. May I know if my approach is logical & correct or is there any other way to do it? Thanks in advance for your help.



![[upsidedown] [upsidedown] [upsidedown]](/data/assets/smilies/upsidedown.gif)
![[bigears] [bigears] [bigears]](/data/assets/smilies/bigears.gif) .
.