Navigation
Install the app
How to install the app on iOS
Follow along with the video below to see how to install our site as a web app on your home screen.
Note: This feature may not be available in some browsers.
More options
Style variation
-
Congratulations TugboatEng on being selected by the Eng-Tips community for having the most helpful posts in the forums last week. Way to Go!
You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
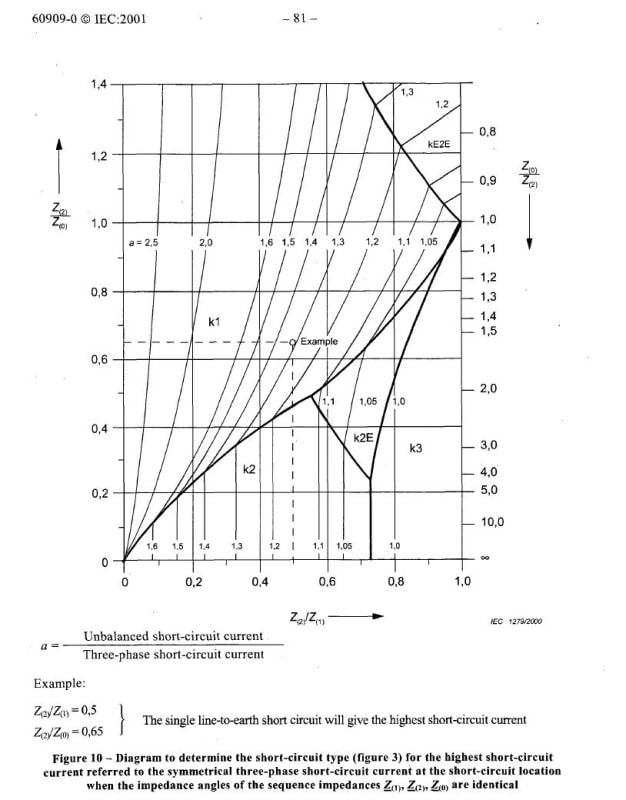
L-L-G VS L-G Fault Level
- Thread starter Cerkit
- Start date
- Status
- Not open for further replies.
mparenteau
Electrical
Location in the circuit? If it's near a transformer secondary, the L-G fault will be higher.
What type of installation is it (can we get a circuit diagram)?
If your installation is near the transformer on the secondary side then L-G should be the same as L-L-G, this is of course under the pretence that all the impedances are equal.
However! Since both L-G and L-L-G are dependent on the zero sequence they are therefore both dependent on the return path for the fault and the transformer/source earthing.
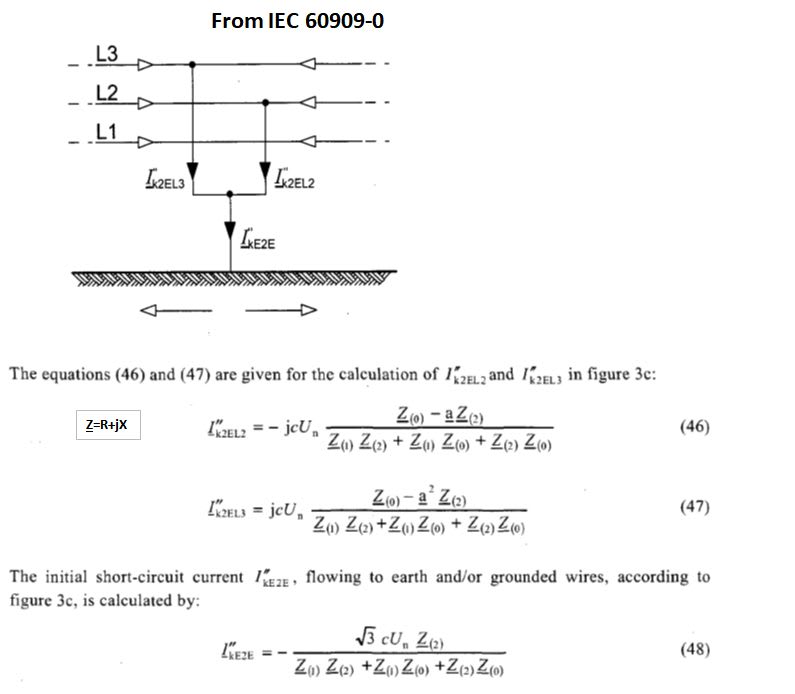
If we strictly look at the equations assuming E is the phase pre-fault voltage they will look like this:
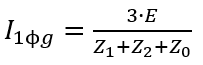
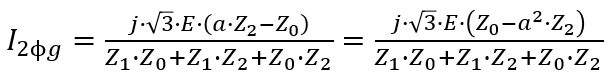
A note about the L-L-G fault, The left and right hand side of the equation corresponds to a faulted phase, so let's say fault current in phase b corresponds to the left equation and phase c to the right equation. Then from a strictly mathematical perspective if Z0 is greater than Z1 or Z2 if they're equal. Then one phase will have a higher fault current than the other, which can be verified in a simulation tool or by just doing the calculation, although they shouldn't vary greatly to a point where this difference is significant. Then there's an entirely different equation that calculates the fault current in the ground
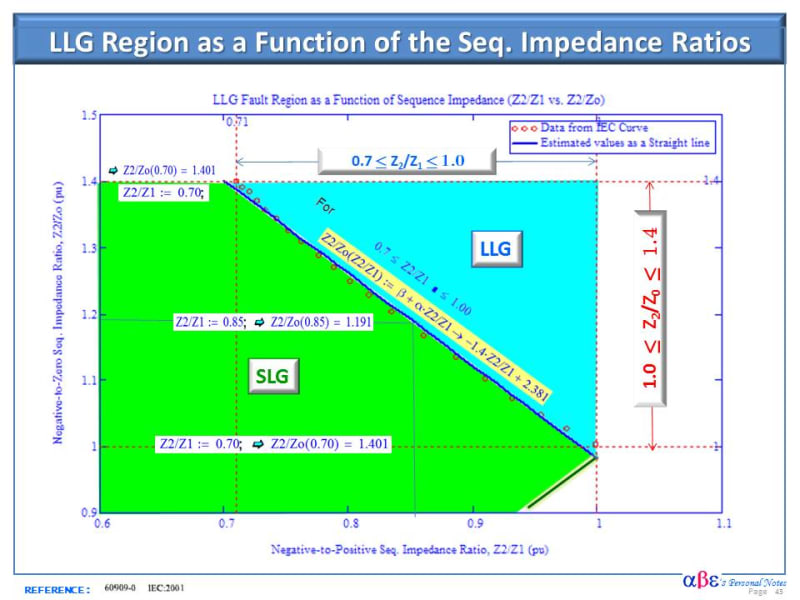
However if all sequence impedances are equal then the L-G and L-L-G faults are equal.
If Z0 is 0, then L-L-G will exceed the L-G short circuit.
All of this however is speaking strictly from a mathematical perspective and not a practical perspective, as I don't have the amount practical experience the majority in this forum has.
The point I'm trying to make: Look at your circuit, where does the fault happen, what's the return path (does it have a high or low impedance?) and what's the system earthing. All of these factors will affect the fault current in the two scenarios you're examining.
If your installation is near the transformer on the secondary side then L-G should be the same as L-L-G, this is of course under the pretence that all the impedances are equal.
However! Since both L-G and L-L-G are dependent on the zero sequence they are therefore both dependent on the return path for the fault and the transformer/source earthing.
If we strictly look at the equations assuming E is the phase pre-fault voltage they will look like this:
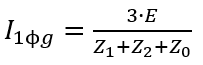
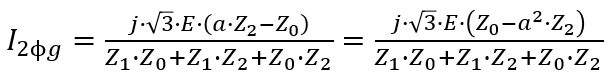
A note about the L-L-G fault, The left and right hand side of the equation corresponds to a faulted phase, so let's say fault current in phase b corresponds to the left equation and phase c to the right equation. Then from a strictly mathematical perspective if Z0 is greater than Z1 or Z2 if they're equal. Then one phase will have a higher fault current than the other, which can be verified in a simulation tool or by just doing the calculation, although they shouldn't vary greatly to a point where this difference is significant. Then there's an entirely different equation that calculates the fault current in the ground
However if all sequence impedances are equal then the L-G and L-L-G faults are equal.
If Z0 is 0, then L-L-G will exceed the L-G short circuit.
All of this however is speaking strictly from a mathematical perspective and not a practical perspective, as I don't have the amount practical experience the majority in this forum has.
The point I'm trying to make: Look at your circuit, where does the fault happen, what's the return path (does it have a high or low impedance?) and what's the system earthing. All of these factors will affect the fault current in the two scenarios you're examining.
If the transformer is WYE (high side)/ delta (low side)then the a L-L-G fault
current on the WYE side is higher than the L-G fault. Typical example is a WYE/delta
transformer connected to the Utility at small distributed energy resource (DER) stations.
current on the WYE side is higher than the L-G fault. Typical example is a WYE/delta
transformer connected to the Utility at small distributed energy resource (DER) stations.
- Status
- Not open for further replies.
Similar threads
- Question
- Replies
- 7
- Views
- 4K
- Replies
- 13
- Views
- 945
- Locked
- Question
- Replies
- 10
- Views
- 1K
- Question
- Replies
- 8
- Views
- 10K
- Replies
- 4
- Views
- 1K