Is the 2% rule for bracing valid for concrete columns? 2

[HanStrulo]

Hi Everyone.

In Appendix 6 of the AISC, the strength and stiffness requirements for bracing are presented with 2% being the rule of thumb.

Is the 2% of vertical load bracing requirement also valid for concrete columns?

Do concrete columns have any special bracing requirements.

Thanks alot!

 

[Settingsun]

do you consider the spring to be performing a bracing function during the portion of the load history for which the spring would be in compression and exerting a destabilizing force on the strut?

Yes

I'm happy to consider elements as having both beneficial and adverse aspects as a way to break down a complex system for understanding.

 

[Settingsun]

Because that would do nothing to address the original point of disagreement which was whether or not elements of the surrounding structure can simultaneously:

1) Deliver destabilizing moments to the column end;

2) Be said to be offering rotational restraint to the column end.

I would say it can, by comparison to pinned column with eccentric loads (eg cantilever beam) which deliver the destabilising moments without any restraint due to the joint stiffness. K<1.

For that purpose, which is the purpose, is the logical point of interest not the point within the load history where:

3) Column end curvatures pass zero and reverse and;

4) Column end moments pass zero and reverse?

If that's your preferred definition, then sure. The opposing column end moments are accompanied by larger mid-height moment than before the end moments become opposing so you have to make the choice that the zero crossing is your definition of the start of restraint. You wouldn't know it if you were watching the mid-height moment.

 

[Settingsun]

2) Larger point: in that setup, it seems to me that you've basically arranged things such that the system would be equivalent at the transition point. In doing so, however, it also seems to me that we've moved the starting line forward in time and have lost our ability to study anything that took place before the transition point.

The two are functionally equivalent except for whether the spring is in compression initially. If one spring provides restraint and the other doesn't, it's a subjective definition that the spring in compression isn't restraint, not objective.

 

[KootK]

I would say it can, by comparison to pinned column with eccentric loads (eg cantilever beam) which deliver the destabilizing moments without any restraint due to the joint stiffness. K<1.

K<1? Is that a misstype? For the cantilever case described, it should should be:

K = 1 for a bifurcation analysis on a column without imperfections and;

K > 1 for most other types of buckling analyses although, for those, the definition of K becomes admittedly fuzzy.

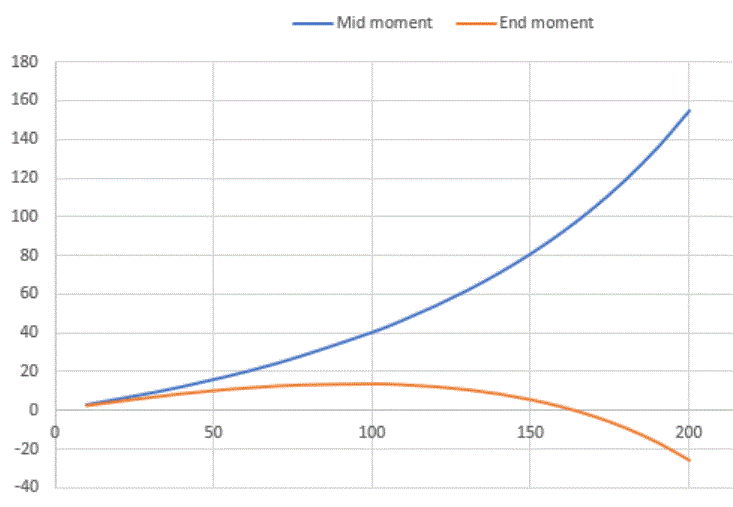
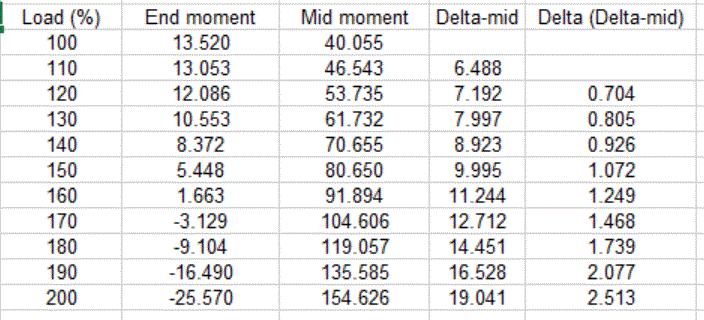
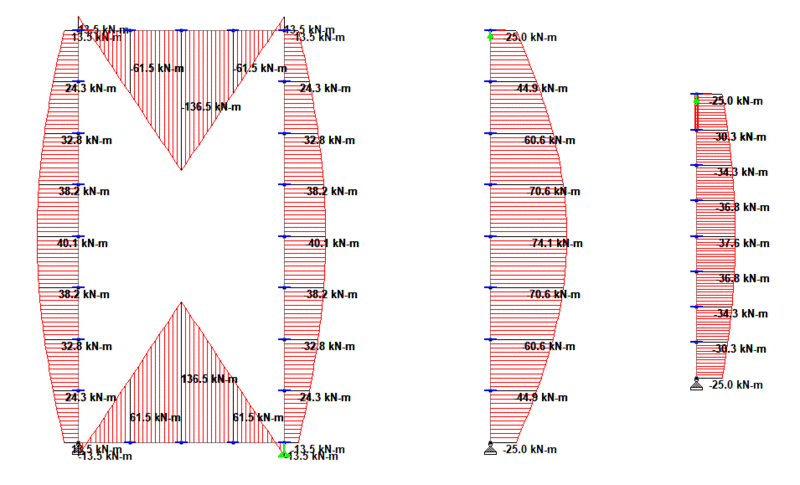
Moreover, I think that the point of maximum clockwise moment on the L-frame actually IS the transition point. You know how, with a plain, pin-pin column the Euler buckling load is the load at which the column is equally happy to buckle 6" to the right, 30" to the right, or 18" to the left? It's similar with the L-frame: at the transition point, the column is equally happy:

1) In single curvature at it's maximum CW end moment;

2) In double curvature at the maximum a CCW end moment that would keep the system in equilibrium at that load level;

3) An infinite number of points in between those extremes including the location where the end moment would be zero.

This is the nature of the column "buckling" in single curvature at the transition point before assuming it's progressing along to the K<1, double curvature buckling mode.

If I'm right about this, which will no doubt be disputed, it just makes the transition point all the more important and less arbitrary, yeah?

 

[KootK]

If that's your preferred definition, then sure. The opposing column end moments are accompanied by larger mid-height moment than before the end moments become opposing so you have to make the choice that the zero crossing is your definition of the start of restraint. You wouldn't know it if you were watching the mid-height moment.

I think that you would know it if you were watching the mid-height moment alone. At least, you would if you were watching it closely enough, measuring the rate of moment increase relative to the increase in the applied load. The mid-height moment will grow at a faster rate when the column is buckling in single curvature than when it is buckling in double curvature. Viewed from an energy perspective, this is one explanation for why the column prefers to buckle in single curvature when that possibility is available.

 

[KootK]

The two are functionally equivalent except for whether the spring is in compression initially. If one spring provides restraint and the other doesn't, it's a subjective definition that the spring in compression isn't restraint, not objective.

I disagree. I think that your functionally equivalent, alternate setup just leads to a functionally equivalent, alternate question.

Before I would have asked: is a brace really performing the bracing function during part of the load history when the brace itself would be destabilizing the thing being braced? ie. until the stretch in the spring relieved the pre-compression in the spring?

Now I would ask: is a brace really performing the bracing function during the part of the load history where the brace would be accompanied by an initial, destabilizing force in the direction of the brace that has not yet been fully offset by the tension developed in the spring as it stretches?

In my opinion, both questions remain unanswered.

 

[KootK]

@steveh49: our current lines of reasoning don't seem to be getting us any closer to a two man consensus. So I'm planning to switch gears and hit this from an energy minimization perspective. It's hardly a sure thing but I've reason to be hopeful. Before I bother with the good stuff, however, I'd like to get some preliminaries out of the way. If you disagree with what I have to say in this post, the rest will just be wasted effort on my part. This is all stuff that I'm confident that I could prove given enough time. That said, I may never get around to actually putting in that time. If it happens that you just agree with this part, sans fuss, that would be peachy.

In reference to the sketch below, and starting with just the point load and no moment, I claim that:

1) The addition of the moment will lessen the deflection at the point of the applied load.

2) Because of #1, the addition of the moment will lessen the amount that the potential energy of the applied load is reduced by the beam deflection.

3) The double curvature created by the moment will increase the total area under the beam moment diagram.

4) Because of #3, the double curvature will increase the amount of flexural strain energy stored in the beam.

5) While respecting equilibrium, structures tend to assume deflected shapes that minimize internal strain energy and facilitate the greatest possible reduction in the potential energy of the externally applied loads. In this sense, structures seek the "lowest cost" means of supporting the loads applied to them.

What do you think of that stuff?

 

[Settingsun]

I think that you would know it if you were watching the mid-height moment alone. At least, you would if you were watching it closely enough, measuring the rate of moment increase relative to the increase in the applied load. The mid-height moment will grow at a faster rate when the column is buckling in single curvature than when it is buckling in double curvature. Viewed from an energy perspective, this is one explanation for why the column prefers to buckle in single curvature when that possibility is available.

Unless we're talking about different things, this isn't correct, so we should clear it up before going further. The images below show the analysis model and graphs of column end moment and column mid-height moment. The frame geometry is 8m x 4m, with 8" x 8" x 0.375" steel square hollow section for all members, braced at top left corner. The x-axis of the graph is % relative to the load case shown; the y-axis is kNm. As an indication of slenderness, the column is in single curvature at uniform 25kNm in the linear analysis of the 100% load case.

I refer back to the image from the British Standard a few posts ago: the second-order component of the end moment is related to the second order increase in mid-height moment. It's a by-product of the second-order column flexure (p-delta) acting against the beam stiffness, and is increasing in magnitude at all times.

 

[Settingsun]

K<1? Is that a misstype? For the cantilever case described, it should should be:

I meant this type of column loading - cantilever beam at column end so there is a rigid joint delivering moment to the column but no beneficial restraint (K=1.0):

Analysis results below, though I modelled the eccentric load as an end moment rather than modelling the cantilever beams. They all have the same axial load and first-order moment (the 100% load case from the previous post, causing 25kNm constant moment as can be seen from the top and bottom moments of the middle and right models.

Left to right: Box frame --> same length column but no end restraint (K=1.0) --> code effective length (K~0.69).

I know this is all nothing new to you, but is the basis for my saying there is restraint to the column in the frame even in single curvature. The restraint is beneficial at all load increments compared to the pin-pin column with eccentric loading.