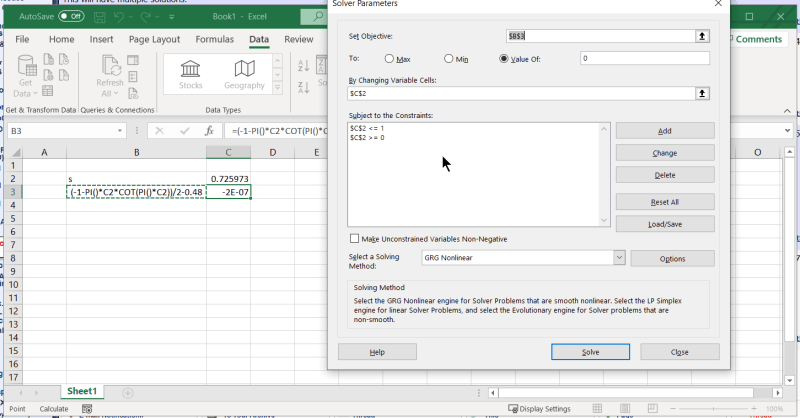
How do I enter the following into an integration calculator to solve for s?
Sum(n= 0 to infinity, s^2/(n^2-s^2)) when the sum value has a known value (i.e. sum() = 0.40348)
Dennis Kirk Engineering
Sum(n= 0 to infinity, s^2/(n^2-s^2)) when the sum value has a known value (i.e. sum() = 0.40348)
Dennis Kirk Engineering