Hello again,
now I a bit more understand what is the purpose of your model - you would like to simulate a crack or even crack propagation(?).
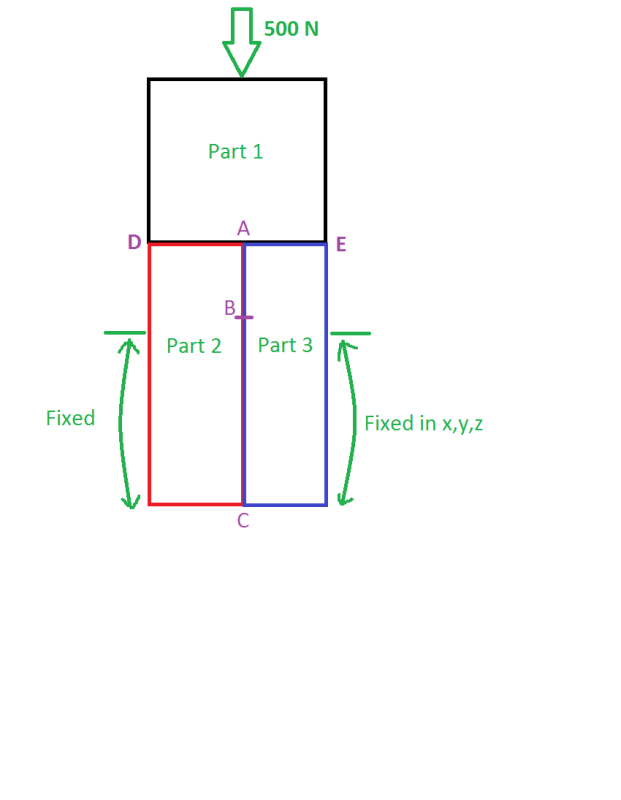
And in your model already initiated crack is between AB.
I guess that unrealistic stress was observed on points A and B, but nothing between, is it so?
Well I afraid it is not so easy...
1. Firstly consider if you really want to simulate it by FEM, maybe BEM could be more convenient - of course I do not know what kinds of solvers are available for you.
2. If this must be done in FEM / NX Nastran, maybe more suitable can be nonlinear SOL601 - although you don't (I think) need to consider nonlinear material, it can be better for convergence because at least you can divide solution to larger number of step.
And there are many function, such as "killing" of elements after exceeding of their defined strength, support of large displacements/strains etc.
BTW, as I wrote you last time:
you used linear static solver SOL 101. Don't believe the results just because there are some - these results cannot be always converged, I mean final (correct, accurate...).
Just open .f06 file and try to find message: CONTACT ITERATION CONVERGED. If there is instead a message something like "the number of iteration was exceeded", then you have unconverged results.
3. I do not know anything about your FE model, but I guess just for approximation to stress/strain results for surrounding A and B, there must be very, very fine mesh...but this geometry is so simply that I would do it by mapped mesh, and then several times refine A and B by element splitting - so there will be only HEXA elements.
You mentioned stress 300.000 MPa - ok, it was on one element, but check the gradient to neighbor - by proper meshing you can decrease it to reasonable value.
@rb1957 - dear rb1957, talking about singularities: sorry I am not a native speaker in English so I don't know precisely what all can be called as singularity in EN. But I guess in 2nd scenario points A and B are actually singular - it is geometrical singularity. Similar to a corner, edge (and 3D they are indeed edges)...and as consequence of this discretisation there is artificial stress peak. Do you agree?
Regards from Prague, guys
Jan
With best regards,
Dr. Jan Vojna
Lead Engineer Development
Siemens, s.r.o.