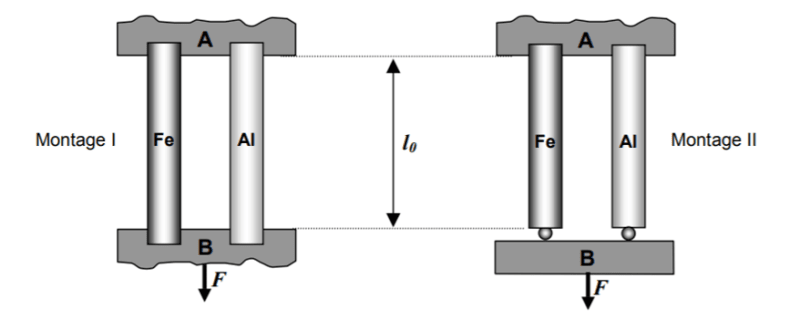
Hello everyone, in one solved problem in Strength of Materials, it was mentioned that the applied force on each bar for montage II is F/2 , even though they're made of different materials : Steel and Aluminum. Can you please explain to me why ? I'd be really grateful .