to determine the flow rate of natural gas in a 10-inch steel pipe that is 5000 feet long, with an inlet pressure of 100 psia and an outlet pressure of 75 psia, we can use the Weymouth equation, which is suitable for high-pressure gas pipelines. According to the context, the Weymouth equation is appropriate for pressure ranges above 100 psi and is given by:
$$
Q = \left(\frac{TB}{PB}\right)^{0.5} \cdot \left(\frac{2 \cdot L \cdot (P1^2 - P2^2)}{\pi^{0.5} \cdot D^{4.167}}\right)^{0.5}
$$
Where:
- \( Q \) is the gas flow rate in cubic feet per day (CFD),
- \( TB \) is the base temperature in Rankine (°R),
- \( PB \) is the base absolute pressure in psia,
- \( L \) is the pipeline length in miles,
- \( P1 \) is the inlet pressure in psia,
- \( P2 \) is the outlet pressure in psia,
- \( D \) is the pipe inside diameter in inches.
Given:
- \( TB = 520 \) °R,
- \( PB = 14.76 \) psia,
- \( L = 5000 \) feet (which converts to approximately 0.9524 miles),
- \( P1 = 100 \) psia,
- \( P2 = 75 \) psia,
- \( D = 10 \) inches.
Substituting these values into the equation, we get:
$$
Q = \left(\frac{520}{14.76}\right)^{0.5} \cdot \left(\frac{2 \cdot 0.9524 \cdot (100^2 - 75^2)}{\pi^{0.5} \cdot 10^{4.167}}\right)^{0.5}
$$
Calculating step by step:
1. Calculate the term inside the first parenthesis:
$$
\left(\frac{520}{14.76}\right)^{0.5} \approx 18.67
$$
2. Calculate the pressure difference squared:
$$
100^2 - 75^2 = 10000 - 5625 = 4375
$$
3. Substitute back into the equation:
$$
Q = 18.67 \cdot \left(\frac{2 \cdot 0.9524 \cdot 4375}{\pi^{0.5} \cdot 10^{4.167}}\right)^{0.5}
$$
4. Simplify the expression inside the second parenthesis:
$$
\frac{2 \cdot 0.9524 \cdot 4375}{\pi^{0.5} \cdot 10^{4.167}} \approx \frac{8357}{100.53} \approx 83.1
$$
5. Finally, calculate the flow rate:
$$
Q \approx 18.67 \cdot \sqrt{83.1} \approx 18.67 \cdot 9.12 \approx 170.4 \text{ CFD}
$$
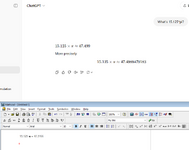
Therefore, the flow rate of natural gas in the 10-inch steel pipe under the given conditions is approximately 170.4 cubic feet per day (CFD)
Great. Now determine the flow rate of natural gas in a 10-inch steel pipe that is 5000 feet long, with an inlet pressure of 1015 psia and an outlet pressure of 75 psia, we can use the General Flow Equation for natural gas. This equation is often derived from the Darcy-Weisbach equation and is commonly used in the industry.
The general form of the equation is:
\[ Q = \frac{C \cdot D^2 \cdot (P_1^2 - P_2^2)}{\sqrt{T} \cdot L \cdot Z \cdot \mu} \]
Where:
- \( Q \) is the flow rate (in standard cubic feet per day, scfd).
- \( C \) is a constant (approximately 1728 for the units used here).
- \( D \) is the inside diameter of the pipe (in inches).
- \( P_1 \) is the inlet pressure (psia).
- \( P_2 \) is the outlet pressure (psia).
- \( T \) is the average temperature (in Rankine, R).
- \( L \) is the length of the pipe (in feet).
- \( Z \) is the compressibility factor (dimensionless).
- \( \mu \) is the viscosity of the gas (in centipoise).
For simplicity, let's assume:
- The average temperature \( T \) is 60°F, which is 520 R.
- The compressibility factor \( Z \) is 1 (for ideal gas approximation).
- The viscosity \( \mu \) is 0.014 cp (a typical value for natural gas).
Given:
- \( D = 10 \) inches
- \( P_1 = 1015 \) psia
- \( P_2 = 75 \) psia
- \( L = 5000 \) feet
- \( T = 520 \) R
- \( Z = 1 \)
- \( \mu = 0.014 \) cp
Substitute these values into the equation:
\[ Q = \frac{1728 \cdot (10)^2 \cdot (1015^2 - 75^2)}{\sqrt{520} \cdot 5000 \cdot 1 \cdot 0.014} \]
First, calculate \( P_1^2 \) and \( P_2^2 \):
\[ P_1^2 = 1015^2 = 1030225 \]
\[ P_2^2 = 75^2 = 5625 \]
Then, calculate \( P_1^2 - P_2^2 \):
\[ P_1^2 - P_2^2 = 1030225 - 5625 = 1024600 \]
Next, calculate the numerator:
\[ \text{Numerator} = 1728 \cdot 100 \cdot 1024600 = 176701440000 \]
Now, calculate the denominator:
\[ \sqrt{520} \approx 22.8 \]
\[ \text{Denominator} = 22.8 \cdot 5000 \cdot 1 \cdot 0.014 = 1602 \]
Finally, calculate the flow rate \( Q \):
\[ Q = \frac{176701440000}{1602} \approx 110300650 \text{ scfd} \]
So, the flow rate of natural gas in the pipe is approximately **110,300,650 scfd**.
I'm gonna go get a beer now.
$$
Q = \left(\frac{TB}{PB}\right)^{0.5} \cdot \left(\frac{2 \cdot L \cdot (P1^2 - P2^2)}{\pi^{0.5} \cdot D^{4.167}}\right)^{0.5}
$$
Where:
- \( Q \) is the gas flow rate in cubic feet per day (CFD),
- \( TB \) is the base temperature in Rankine (°R),
- \( PB \) is the base absolute pressure in psia,
- \( L \) is the pipeline length in miles,
- \( P1 \) is the inlet pressure in psia,
- \( P2 \) is the outlet pressure in psia,
- \( D \) is the pipe inside diameter in inches.
Given:
- \( TB = 520 \) °R,
- \( PB = 14.76 \) psia,
- \( L = 5000 \) feet (which converts to approximately 0.9524 miles),
- \( P1 = 100 \) psia,
- \( P2 = 75 \) psia,
- \( D = 10 \) inches.
Substituting these values into the equation, we get:
$$
Q = \left(\frac{520}{14.76}\right)^{0.5} \cdot \left(\frac{2 \cdot 0.9524 \cdot (100^2 - 75^2)}{\pi^{0.5} \cdot 10^{4.167}}\right)^{0.5}
$$
Calculating step by step:
1. Calculate the term inside the first parenthesis:
$$
\left(\frac{520}{14.76}\right)^{0.5} \approx 18.67
$$
2. Calculate the pressure difference squared:
$$
100^2 - 75^2 = 10000 - 5625 = 4375
$$
3. Substitute back into the equation:
$$
Q = 18.67 \cdot \left(\frac{2 \cdot 0.9524 \cdot 4375}{\pi^{0.5} \cdot 10^{4.167}}\right)^{0.5}
$$
4. Simplify the expression inside the second parenthesis:
$$
\frac{2 \cdot 0.9524 \cdot 4375}{\pi^{0.5} \cdot 10^{4.167}} \approx \frac{8357}{100.53} \approx 83.1
$$
5. Finally, calculate the flow rate:
$$
Q \approx 18.67 \cdot \sqrt{83.1} \approx 18.67 \cdot 9.12 \approx 170.4 \text{ CFD}
$$
Therefore, the flow rate of natural gas in the 10-inch steel pipe under the given conditions is approximately 170.4 cubic feet per day (CFD)
Great. Now determine the flow rate of natural gas in a 10-inch steel pipe that is 5000 feet long, with an inlet pressure of 1015 psia and an outlet pressure of 75 psia, we can use the General Flow Equation for natural gas. This equation is often derived from the Darcy-Weisbach equation and is commonly used in the industry.
The general form of the equation is:
\[ Q = \frac{C \cdot D^2 \cdot (P_1^2 - P_2^2)}{\sqrt{T} \cdot L \cdot Z \cdot \mu} \]
Where:
- \( Q \) is the flow rate (in standard cubic feet per day, scfd).
- \( C \) is a constant (approximately 1728 for the units used here).
- \( D \) is the inside diameter of the pipe (in inches).
- \( P_1 \) is the inlet pressure (psia).
- \( P_2 \) is the outlet pressure (psia).
- \( T \) is the average temperature (in Rankine, R).
- \( L \) is the length of the pipe (in feet).
- \( Z \) is the compressibility factor (dimensionless).
- \( \mu \) is the viscosity of the gas (in centipoise).
For simplicity, let's assume:
- The average temperature \( T \) is 60°F, which is 520 R.
- The compressibility factor \( Z \) is 1 (for ideal gas approximation).
- The viscosity \( \mu \) is 0.014 cp (a typical value for natural gas).
Given:
- \( D = 10 \) inches
- \( P_1 = 1015 \) psia
- \( P_2 = 75 \) psia
- \( L = 5000 \) feet
- \( T = 520 \) R
- \( Z = 1 \)
- \( \mu = 0.014 \) cp
Substitute these values into the equation:
\[ Q = \frac{1728 \cdot (10)^2 \cdot (1015^2 - 75^2)}{\sqrt{520} \cdot 5000 \cdot 1 \cdot 0.014} \]
First, calculate \( P_1^2 \) and \( P_2^2 \):
\[ P_1^2 = 1015^2 = 1030225 \]
\[ P_2^2 = 75^2 = 5625 \]
Then, calculate \( P_1^2 - P_2^2 \):
\[ P_1^2 - P_2^2 = 1030225 - 5625 = 1024600 \]
Next, calculate the numerator:
\[ \text{Numerator} = 1728 \cdot 100 \cdot 1024600 = 176701440000 \]
Now, calculate the denominator:
\[ \sqrt{520} \approx 22.8 \]
\[ \text{Denominator} = 22.8 \cdot 5000 \cdot 1 \cdot 0.014 = 1602 \]
Finally, calculate the flow rate \( Q \):
\[ Q = \frac{176701440000}{1602} \approx 110300650 \text{ scfd} \]
So, the flow rate of natural gas in the pipe is approximately **110,300,650 scfd**.
I'm gonna go get a beer now.
Last edited: