Horizontal and Vertical Deflections due to Concentrated Load

[adharma0]

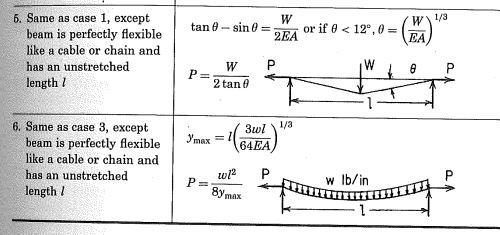
Hello guys...I am trying to find the correct equation to calculate horizontal reaction (H) in the cable due to its self weight (w) and also a concentrated load (P) that is applied horizontally.

The cable is spanned horizontally and the span length is 50 feet (fixed both ends) and the diameter of the cable is, say 0.177 inch (w= 0.084 lb/ft). I would like to limit the maximum vertical deflection (vertical sag due to self weight of the cable) to, say 3 inches at mid-span. Also, there is a concentrated load that is being applied "horizontally" on the cable: P (horizontal) = 200 lb. I would like to limit the "horizontal deflection" to be no more than 1 inch at the location of the applied concentrated "horizontal" load (P). What is the correct formula that I should use to calculate the horizontal force "H" at each end of the cable knowing that I have a horizontal concentrated load (P) and a uniform self-weight (w) of a cable? I do not have any specific steel cable in mind; therefore, I am open to suggestion regarding what kind of steel cable I should use in order to make sure that the horizontal reaction at the end of the cable (H) is lees than the breaking strength of the cable. Please tell me the material properties of the steel cable if you have any suggestion.

Thank you.

 

[manstrom]

PTI has a white paper on something similar. This should be the droid you are looking for..

http://www.post-tensioning.org/Uploads/Technote14.pdf

When I am working on a problem, I never think about beauty but when I have finished, if the solution is not beautiful, I know it is wrong.

-R. Buckminster Fuller

 

[JAE]

Does this help?


Check out Eng-Tips Forum's Policies here:
faq731-376

 

[JAE]

Check out Eng-Tips Forum's Policies here:
faq731-376

 

[BAretired]

Where is the horizontal force applied? At the middle of the cable?

JAE has shown solutions for vertical concentrated load and uniform load but not for horizontal concentrated load.

Under cable weight alone, using the formula by JAE, the reaction force P is 105# if the sag is 3".

Adding a horizontal force of 200# anywhere in the span would cause one horizontal reaction to exceed the other by 200# but the effect of combining a horizontal force with cable weight cannot be superimposed because vertical sag is modified with the addition of the horizontal force. Also, the stretch in the cable will have an effect on sag and needs to be taken into account.

BA

 

[Denial]

Even under self weight alone, you have a fairly taut cable if you want to achieve your <[&nbsp;]3[&nbsp;]inch deflection criterion.[&nbsp;] With self weight of only 4[&nbsp;]lbf, you could safely neglect it when looking at a vertical force of 200[&nbsp;]lbf.[&nbsp;] I suspect it is equally valid to neglect it when the horizontal force is horizontal (and transverse to the cable), but I haven't thought very hard about that.

However you need to clarify what you mean by a horizontal deflection of only 1[&nbsp;]inch. Is this in addition to the 3[&nbsp;]inch deflection in the unloaded state?[&nbsp;] Because that 3[&nbsp;]inches will very readily swing from vertical to horizontal once the horizontal load is applied.[&nbsp;] If the "total horizontal deflection" is to be restricted to 1[&nbsp;]inch you will need a REALLY taut cable.

The fact that the cable has to be taut merely to achieve the 3[&nbsp;]inch criterion when unloaded means that cable extension will be significant and will have to be taken into account in your calculations (as it is in the formulae JAE provided).

Incidentally, your stated values of 0.177[&nbsp;]inch diameter and 0.084[&nbsp;]lbf/ft self-weight require that your cable actually be a solid steel bar. You are much more likely to be using some sort of twisted wire rope.[&nbsp;] If so, the effective area will be less than pi*D²/4 due to the way the overall cross section is made up, and the effective E[&nbsp;]value will be lessened by the fact that the individual strands are run in a spiral rather than straight from end to end.[&nbsp;] The combination of both these effects means that the effective value of A*E will probably lie between 0.2 and 0.55 time the nominal value.[&nbsp;] In the absence of specific information from the manufacturer of the wire rope, use the least favourable value in this range.

 

[BAretired]

Consider a weightless cable with a horizontal force applied at point B half way between support points A and C which are 50' apart.

If the length of cable is L before any load is applied then if it is deflected downward at point B without straining the cable, the sloping length AB and BC will each be L/2. The sag at point B will be:

y = [(L/2)²-(25)²]^1/2 (Pythagoras).

If force H is applied to point B, neglecting any strain in the cable as a result of load, point B will move vertically upward a distance y and horizontally (L/2-25) towards support C. Section AB will have a stress of H while section BC will be unstressed.

Combining this result with the cable weight and cable elongation requires the application of statics and geometry.

BA

 

[Denial]

BAretired's result can be generalised to accommodate cable stretch.
Let L be the unstretched length of the cable (as per BAret).
Let D be the distance between the two attachment points.
Let P be the transverse load.
Let Y be the transverse deflection (as per BAret).
Let T be the cable tension.
Let AE be the usual.

GEOMETRY tells us that
L[1+T/(AE)] = 2*[(D/2)²+Y²]^1/2

STATICS tells us that
P = 2T*sin(theta) ~= 4TY/D
(for small theta)

Combine these to eliminate T and you get
L[1+PD/(4YAE)] = 2*[(D/2)²+Y²]^1/2
which can be solved (numerically) for Y.

Alternatively, eliminate Y and solve for T.

By way of (limited) confirmation, if you set L equal to D is it quite simple to derive the "small theta" case that JAE gives above. (But what is magic about 12°?)

 

[adharma0]

To "manstrom, "JAE", "BAretired", and "Denial", I would like to thank all of you for your responses. I now have a better understanding on how to proceed.