Foundation design with applied moment at top of pedestal

[LearnerN]

I am considering a square footing design for a tall vertical vessel, the vessel of which will yield an applied moment at the top of footing pedestal due to wind load and such along the tall vertical vessel. (I'm a fairly new structural engineer and will have my design reviewed by another engineer, but I learn a lot asking questions on this forum to several different engineers.) In terms of concrete design specifically, there are two main considerations for this type of foundation with an applied moment that are different than a square footing with only a vertical load: (1) effect of applied moment on the punching shear (and one-way?), (2) design of pedestal/pier for flexure. Anything else that's different than for a square footing with only a vertical load?

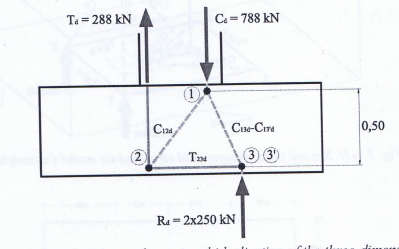
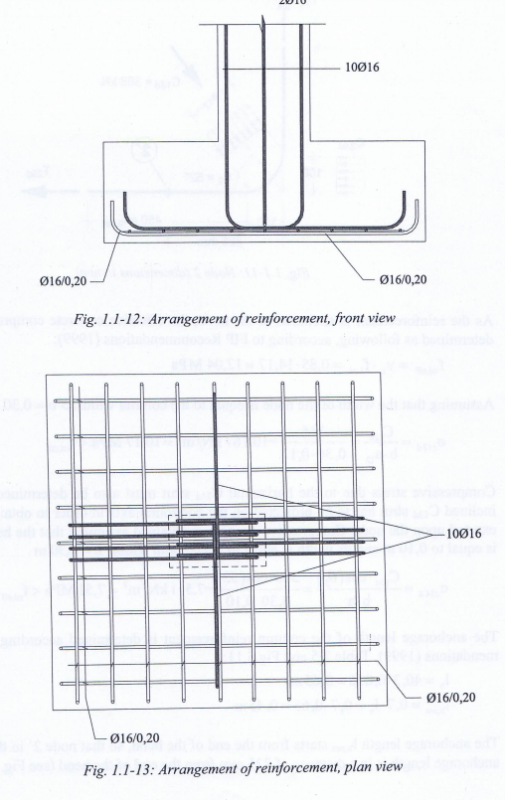
My second question is specifically regarding the punching shear calculation as found in section 8.4.4 of ACI 318-14, and specifically the equations in 8.4.4.2.3. My understanding is that this is how to calculate the max factored two-way shear stress due to having an applied moment on the top of the footing pedestal (see Fig R8.4.4.2.3). Per Table 8.4.2.3.4 for an interior column, if it's a square column (b1=b2) with a nonprestressed slab (ie "footing", since it's talking about the slab-column connection), then gamma_f would be 1...which means gamma_v would be 0 (per 8.4.4.2.2), which means vu_ab or vu_cd would only be equal to v_ug since the other term in this equation would be 0 due to gamma_v being 0. If I'm correct in my understanding so far, this makes no sense to me because then the applied moment would contribute nothing to the two-way shear stress, right? Let me know if I'm totally off-base in my understanding of this section of the code. Thank you.

 

[JStephen]

In the past, using ACI-318-05, it had no provisions for punching shear due to moment. So I'd calculate edge load around the perimeter, convert that to an equivalent uniform load giving the same edge loading, and check shear with that load as well.

 

[KootK]

First, let's get the easy punching shear stuff out of the way.

Per Table 8.4.2.3.4 for an interior column, if it's a square column (b1=b2) with a nonprestressed slab (ie "footing", since it's talking about the slab-column connection), then gamma_f would be 1

I believe that gamma_f calcs out to 0.75. And that value is a maximum. So gamma_f will range between 0.6 and 0.75 at your discretion which should solve the rest of your punching shear issues.

Anything else that's different than for a square footing with only a vertical load?

In my opinion:

1) You may need top steel in your footing if you need to rely on footing self weight or soil overburden for stability.

2) You probably need concentrated footing bottom steel in the vicinity of your column.

3) You need to carefully detail and design the moment transfer joint where your pedestal meets your footing.

It's instructive to consider your situation turned upside down in which case it becomes very similar to a roof slab to column connection. And, like that connection, the Achilles heel of it is moment transfer through the joint. If the punching shear equivalent of P/A + M/S resulst in no net tension in the joint, then a punching shear check as you described in your initial post is appropriate.

If there is net tension, however, then I question whether punching shear is truly the appropriate check to be applied. In such a situation, I recommend strut and tie joint design in place of punching shear / sectional flexure design. To execute the strut and tie design profitably, you'll probably want to set up a spreadsheet. The illustrations below show an example of an appropriate strut and tie model as well the kind of detailing that results. However, as a proud North American, I don't hook my footing rebar at the ends.

I like to debate structural engineering theory -- a lot. If I challenge you on something, know that I'm doing so because I respect your opinion enough to either change it or adopt it.