Equivalent Static Load of a Dynamic Load

[Adriano1367]

First time using this forum, so I hope I'm following proper protocol.

Here is the question: what is the static load equivalent of 7.231 G's?

Here are the details:
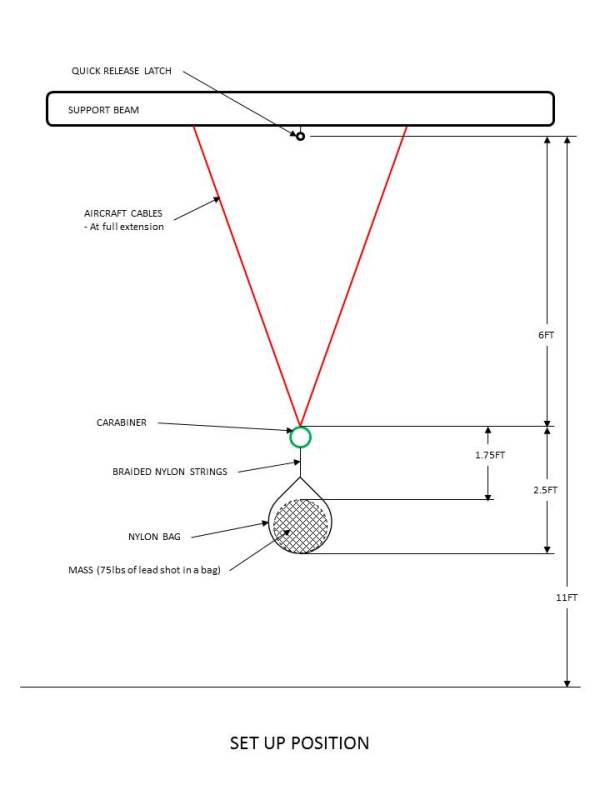
Load = 75 lbs with 4 strings to connect to drop test aparatus
Drop height = 6 feet using 2 aircraft cables (DIA = 0.375")
Protocol
- 2 cables are 36 inches apart at the release height - approximately 11 feet in the air
- cables are then lowered to their full extension to form a single connection point - 6 feet from release point
- load strings are connected to cables via carabiner
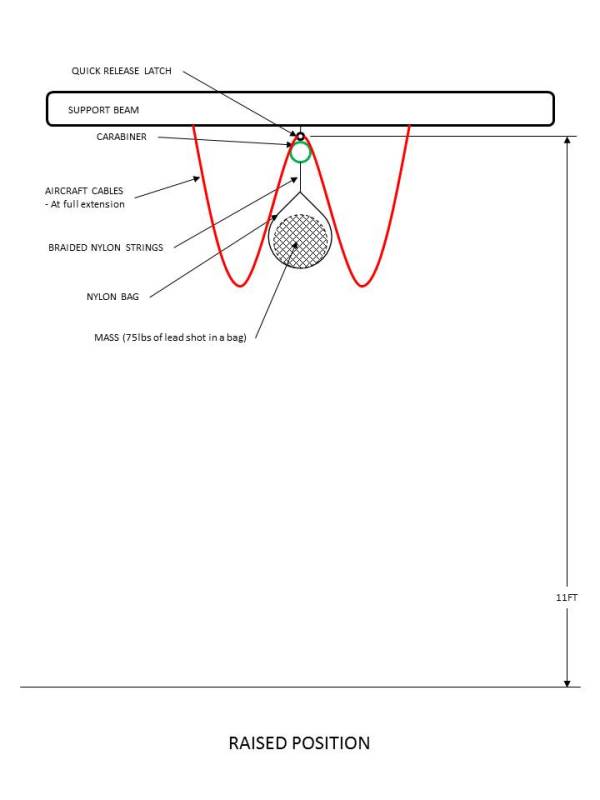
- load is raised and then connected to quick release latch using the carabiner, approximately 11 feet high
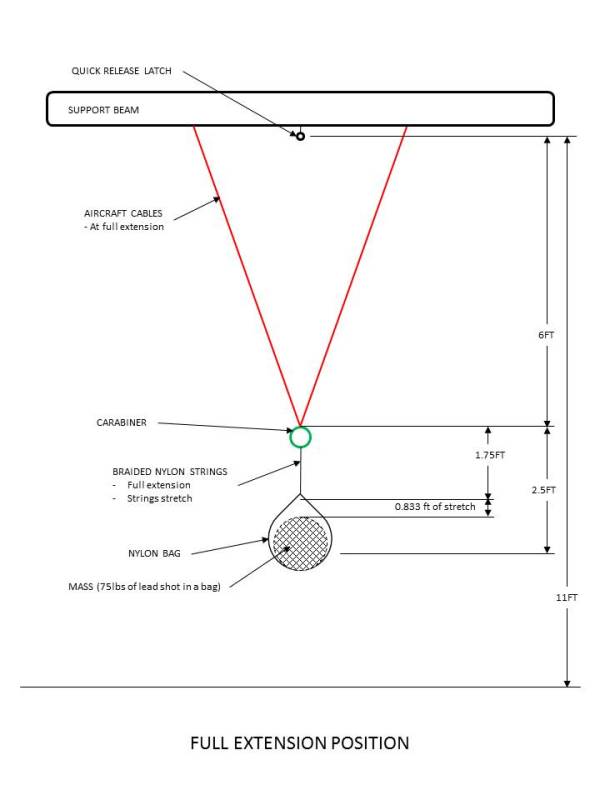
- load is released and falls freely until cables begin the deceleration when the 6 foot length is reached
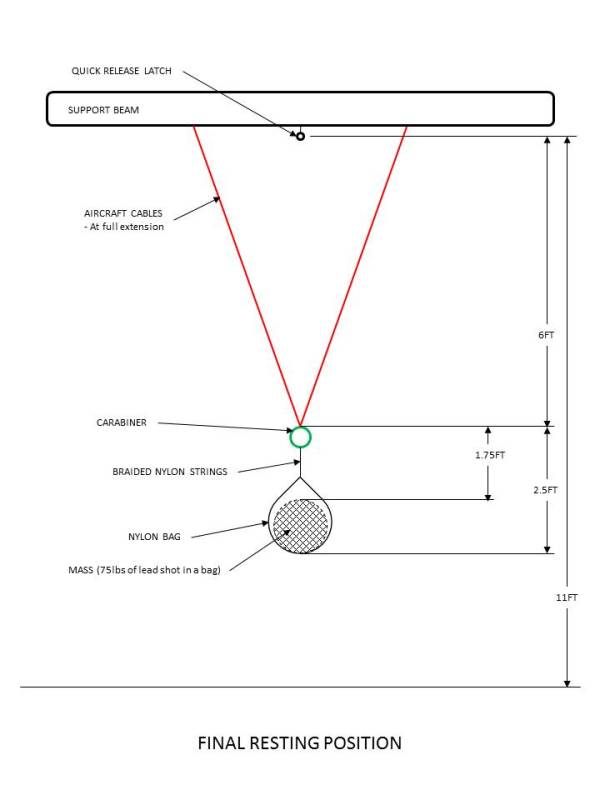
- load strings and cables are elastically stretched, then load bounces 2 more times before it comes to rest - approximately 4 feet off the ground
Calculations - my calculations, using my limited memory of statics and dynamics, yield the following
- Max impact force = 542.325 lbs force
- Approximately 7.231 G's
- Impact velocity = 19.66 ft/sec
- Drop height = 6 ft
- Deceleration distance = 0.8333 ft
- Rate of deceleration = 232.841 ft/sec^2

I am currently using an exceptionally large I-beam to support the test apparatus and would like to build a test rig to conduct this test. Therefore, I'm looking for a static load equivalent so I can decide if a #6 SCHED 40 pipe would sufficiently support the test with the dynamic loads and weight specified.

Any assistance and/or direction would be greatly appreciated...thanks in advance.

 

[rb1957]

ok, so the mass has 5' of free fall, then 6' of resisted fall. The cables are very springy to stretch so much ! but you can calc the strain energy in them, hence the KE of the mass at impact. The mass bounces, so it hit with quite some velocity (the cables weren't acting like arrestor cables on a carrier !! and I suspect that the mass absorbed some of the impact (elastically deformed ?). So there's still an impact to consider and peak load depends on the time to decelerate and the time to accelerate (upside of the bounce).

another day in paradise, or is paradise one day closer ?

 

[Adriano1367]

Hi rb1957,

After reading my post again, I think my explanation wasn't very clear, so I will add some more details.

Mass (load) will be at rest in the air, s0 = 11 feet above the ground
Mass will be released in free fall and accelerate due to gravity until the cables are extended, just prior to the strings starting to stretch, s1 = -6 feet which is 5ft above ground
Mass decelerates when there is initial tension on the cables to its full extension point with the strings stretched to their max point, delta s = -0.833 ft which is
- cables are acting as an arrestor
- this stretch is due to the elasticity of the 4 load strings, not the cables
- the mass is held inside of a nylon bag with 4 strings, the strings are attached to the quick release latch that is 11 feet in the air
Mass has negligible deformation because it does not impact any object
- after 2-3 rebounds of decaying height the final position is sf = 5 feet above the ground

I assume peak load to be at the point when the mass has completed its free fall and deceleration, which would be -6ft of free fall plus -0.833 of elastic deformation of the load strings (11ft -6ft - 0.833ft = 4.167ft above the ground). This is the static load equivalent that I am looking for so that I can determine the correct size of structural steel or tubing to mount the cables for this "drop test"

 

[drawoh]

Adriano1367,

Energy is easy to calculate. You lift 75lb weight a distance of 6ft, then you drop it. 6ft[×]75lb=450lb.ft. This is kinetic energy, and it becomes the strain energy your cables must absorb. This is the easy way to work out your terminal velocity. If you know how elastic your cables are, you can work out force using strain energy.

0.8333ft is ten inches. Do you really have Ø.375" cables that stretch 10in over six feet?

I don't like the term "equivalent static load". How about maximum deceleration force?



--
JHG

 

[77JQX]

Using Hooke's Law I get 1230 lb max force.

 

[rb1957]

I think it odd that the final resting altitude is the same as maximum stretch in the cables (5' above ground) ?

the cables are always attached to the mass, right ? what altitude is the anchor for the cables ? I'm trying to picture slack cables at 11', and taunt at 5' ?

at t=0 the energy in the system is the PE of the mass. initially the mass falls free-fall, then the cables start arresting the fall, until at 5' the velocity of the mass is 0 and the change in PE of the mass has been converted into strain energy of the cables. This strain energy powers the rebound.

another day in paradise, or is paradise one day closer ?

 

[Adriano1367]

All,

The cables do not stretch. It is the 4 braided nylon load strings and the nylon bag that is holding the mass that stretches.

The full extension position of the load is 0.833ft below the 6ft extension... 6.833ft below the 11ft starting height or 4.167ft (5ft - 0.833ft) above the ground. I've attached some crude sketches ... not to scale ... of the 4 positions of the test, reference image 3.

77JQX,
Just so I understand ... 1230lbs of force for both cables (615lbs x 2 cables) at the max load, i.e., when the 75lb mass has reached the full extension shown in image 3

Thanks for all the input and feedback so far!!

 

[rb1957]

so the mass starts to fall, the cables unravel (without load).
then the cables deploy to full length, with the mass travelling due to free fall.
then the braided nylon strings the fall (cables assumed rigid), and the mass stops falling shortly afterwards.

it sounds like you're trying to subject the contents of the bag to a finite acceleration ?

it would've been nice to start with the picture ... much clearer.

another day in paradise, or is paradise one day closer ?

 

[drawoh]

Adriano1367,

You can solve this using energy methods. Your eleven foot height is irrelevant.

You lift 75lb to a height of six feet. The work done E_w=6ft[×]75lb=450ft.lb. This now is potential energy, E_p=E_w=450ft.lb.

You release the mass and it drops back down the six feet, extending the cables. Your kinetic energy now is E_k=E_p=450ft.lb.

Your mass decelerates to a halt, converting all the kinetic energy to strain energy, E_s=E_k=450ft.lb.

The distance traveled while decelerating is .83333ft. The work done is E_s=x_d[×]F_average.

The average force F_average=E_s/x_d=450ft.lb/.8333ft=540lb.

The maximum vertical force will be twice that, F_max=2[×]540lb=1080lb.

This is distributed between the two cables. The cables see a higher force because your load is the vertical component of the actual force vectors, which would be affected by the separation at the top of the cables, which you did not specify.

Does this look right, everyone?

--
JHG

 

[77JQX]

I used a fall distance of 6.8333 feet, rather than 6 feet. And I integrated kxdx, to solve for the spring constant, rather than the simpler method applied by drawoh. Using 6.833 feet, drawoh's method also gives 1230 lb. I think we're in agreement.

 

[drawoh]

77JQX,

The .83333ft deflection is a dynamic condition that occurs momentarily, due to the maximum deceleration force. At static equilibrium, the force will be 75lb, and the deflection as per my numbers, .833333ft/1080lb[×]75lb=.058ft, or about 0.7in. You are lifting the weight 6.058ft, not 6.83333ft. That changes my calculated force to 1090lb.

--
JHG

 

[Adriano1367]

Hi drawoh and 77JQX,

Thanks for your input!!

The cables are 3ft apart, or each cable is 1.5ft from vertical (my apologies, should have included this in the sketches).

This gives an angle of approximately 14° between vertical and the actual force vector of 545 lbs.

If I have calculated correctly, this would yield a vertical vector of approximately 561.7 lbs for each cable and total of 1123.4 lbs.

Does this sound correct?

AFD