atkrank
Mechanical
- May 24, 2016
- 2
I am modifying an industrial dust collection system that has multiple pick up spots and I am desperate for some enlightenment. The original designed system has 28 pick up locations with the round duct size varying from 6" to 13". It was designed according to NFPA standards such that for each branch of duct, the velocity needs to be between 4,000-5,0000cfms. I have a schedule to which the original system was designed that states the size, vol. flow rate, and the velocity.
It seems the way they originally designed it was that they picked an arbitrary flow rate at each pick-up or derived a flow rate from a collection hood calculation, then picked duct sizes until the duct velocity was within the allowable limits.
The issue is that during construction one of the pick-up locations was capped off due to geometric constraints and has been capped ever since. So my first questions is that since this duct is capped off, would that increase all the other pick-up flow rates by an equal cmf to make up the difference for the capped end? Or would it favor the larger ducts more than the smaller ones because of friction/restriction?
All this duct work is old and damaged and is being re-placed. So I thought now would be the perfect opportunity to hook up the capped pick-up by reducing the duct to a smaller size and designing a new hood. My hood design re-quires a flow rate of at least 3,000cfm to be able to capture the dust. The original schedule for this location was 4,000cfm with a 13" duct. Would reducing the duct size change the flow rate? If so, which equations/principles would I use to calculate this new duct size and would the 1000cfm difference be split equally amongst the other 27 pick-up spots? Or would I consider the flow rate to be conserved and just the velocity increases? I do not think the latter would be the case but I would like someone else to be able to verify. Maybe even run through an easy example? Thanks!
Here is an arbitrary sketch I drew to demonstrate the concept. This is not the actual situation:
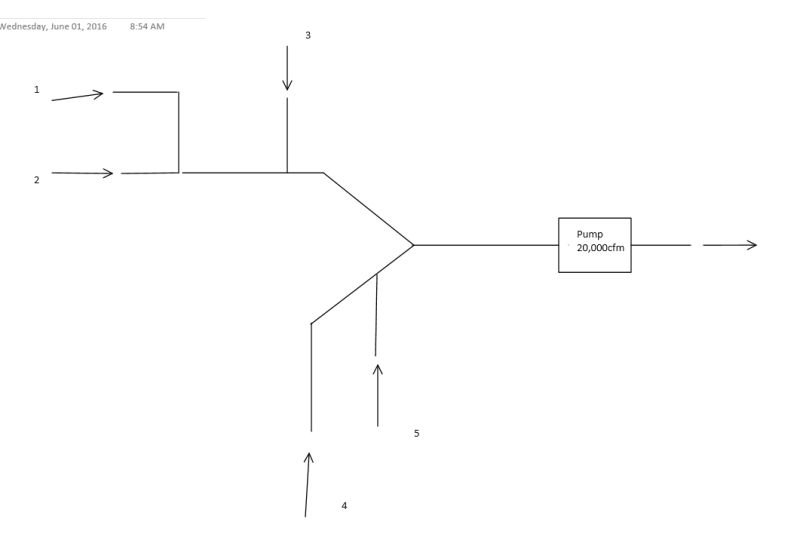
It seems the way they originally designed it was that they picked an arbitrary flow rate at each pick-up or derived a flow rate from a collection hood calculation, then picked duct sizes until the duct velocity was within the allowable limits.
The issue is that during construction one of the pick-up locations was capped off due to geometric constraints and has been capped ever since. So my first questions is that since this duct is capped off, would that increase all the other pick-up flow rates by an equal cmf to make up the difference for the capped end? Or would it favor the larger ducts more than the smaller ones because of friction/restriction?
All this duct work is old and damaged and is being re-placed. So I thought now would be the perfect opportunity to hook up the capped pick-up by reducing the duct to a smaller size and designing a new hood. My hood design re-quires a flow rate of at least 3,000cfm to be able to capture the dust. The original schedule for this location was 4,000cfm with a 13" duct. Would reducing the duct size change the flow rate? If so, which equations/principles would I use to calculate this new duct size and would the 1000cfm difference be split equally amongst the other 27 pick-up spots? Or would I consider the flow rate to be conserved and just the velocity increases? I do not think the latter would be the case but I would like someone else to be able to verify. Maybe even run through an easy example? Thanks!
Here is an arbitrary sketch I drew to demonstrate the concept. This is not the actual situation:

