Discharge Pressure in a centrifugal pump 1

[grey84]

Hi everyone.
I have a question about the discharge pressure of a centrifugal pump at fixed speed.
The pump is in discontinuos service and has to transport the liquid from a blanketing vessel to another blanketing vessel (with constant operating pressure)
through a line without control valve.
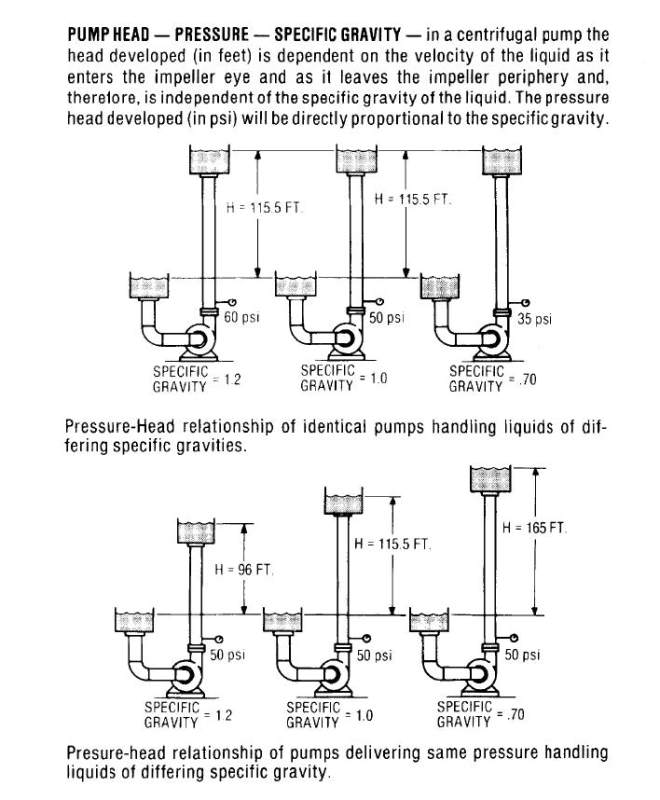
I have sized the pump for a flowrate of a liquid with a certain density; so i have obtained a head H1 and an associated discharge pressure p1.
Now, if i change the pumped fluid, with a more dense fluid with the same viscosity, the pump head and the volumetric flowrate remains the same,
but the discharge pressure become higher. So what is the pressure profile in the line considering the friction losse are more or less the same in the two cases,
where is the mistake?

thanks

Red.

 

[EmmanuelTop]

You have answered your question yourself.
Also remember to size the pump motor for the high-density fluid operation.

Dejan IVANOVIC
Process Engineer, MSChE

 

[bimr]

The specific gravity of a liquid does not change the centrifugal pump curve. Specific gravity affects the HP required to turn the pump at the required speed. Correcting for HP requirements for liquids with a specific gravity is calculated using:

BHP = GPM X Head X Specific Gravity / 3960 x Pump Eff

Changes in the specific gravity will affect pressure loss and flow rates in pipelines.

 

[LittleInch]

The "mistake" is in assuming that the higher density fluid has the same viscosity as the lower density fluid and hence for the same flow rate the same head loss occurs, As bimr has pointed out pressure is a function of head and density and as density increase so does the pressure of the same head. The power required to pump a higher density fluid than another at the same flowrate requires a higher power input.

for many, but not all, liquids a higher density fluid has a higher viscosity, hence for the same flow rate the head losses increase and so the pressure losses increase even further than the releative bensities.



Remember - More details = better answers
Also: If you get a response it's polite to respond to it.

 

[Compositepro]

Don't make the common mistake of confusing head with pressure. Head is the height of the liquid column in feet and pressure is in psi. Head stays constant as fluid density changes but pressure does not.

 

[grey84]

Thank you for the answers.
I'll try to explain better my question.
First case: I pump a liquid with a density of 700 kg/m3 in a vessel working at constant pressure of e.g. 10 barg.
The pump works on a specific operating point, that is the intersection between the pump curve and the system curve;
at this point correspond e.g. a discharge pressure of 15 barg.
Second case: I want to pump, with the same pump in the same system, a liquid with a density of 1000 kg/m3 and the same viscosity of the first case;
the operating point will be the same, so i'll have the same volumetric flow and the same pump head with a higher discharge pressure of e.g. 20 barg.
So, in the first case i have a dp of 5 bar from the pump outlet nozzle and to final vessel, in the second case a dp of 10 bar.
I don't understand how the pressure will be balanced in the second case; i have a higher discharge pressure but the final pressure it's the same,
the flow rate is the same (the pump work on the same operating point), and friction loss are the same.
If i had a control valve, i guess that the fluids would arrive upstream the valve with different pressure in the two cases, but i'd have the same
pressure downstream the control valve.

 

[EmmanuelTop]

If there are no means of controlling flow in this loop, the pump will simply follow its curve. In the theoretical case you described, without control valve (or pump speed control), the pump will end up operating at the point where the differential head developed by the pump is equal to the system resistance (plus the head difference between the receiver and the source vessel). So we can not say that flows will be identical in both cases - given the different physical properties of fluids and different driving forces available for flow (pressure differential) in the two cases. If a control valve is installed downstream of the pump, then yes - the valve will see different pressures upstream and similar pressures downstream, for identical flows.

The only way one can picture this to him/herself is if a real example is worked out, with real fluids and real pipework.



Dejan IVANOVIC
Process Engineer, MSChE

 

[LittleInch]

Ok,

It's taken me a while, but I now have it (I think)

For your example, it won't work. The end pressure when converted to m heqad, changes, so it isn't the same.

10 bar at an SG of 0.7 = approx. 142m head of your liquid. Your 15 bar = approx. 214 m - head difference of 72m

10 bar at Sg of 1 = approx. metres head of 100m, Assuming your pump can handle it, the head stays the same (214) and the pressure goes up to 21.4 barg. You now have ahead difference of 114m. Unless the laws of physics have changed when I wasn't looking, for the same pipe with a fluid of the same density but different head differences, the flow CANNOT be the same. Therefore your statement "so I'll have the same volumetric flow " is not possible unless , as ET says, you put in extra pressure difference by means of a control valve.

Therefore the flow will increase until the resistance matches the pump discharge, which will then decrease as flow increase. Power though will probably end up double - higher density and more flow.

Makes sense?

Remember - More details = better answers
Also: If you get a response it's polite to respond to it.