Differences between calculation and reality 3

[m.piron]

Good morning.
I have the structure in picture. The material of the beam is steel S235.

The real F is 350N, but I continuosly put and remove the load, so I take into account 2*F (found by match the elastic and potential energy, 0.5*k*x^2 = m*g*x).
I found a stress of 453 MPa, so this beam couldn't carry the load.

My question is, I'm using this beam every day, and it's not broken, nor bend.
Why it resist?
What is wrong in my calculation?

Thanks

 

[Tomfh]

I think the problem is because he has misinterpreted the parameters, k & x for instance, in equating the moment and energy, thus the wrong conclusion - "2*F".

Yes, exactly. He’s concluded that F = 2F, which is clearly wrong.

 

[BAretired]

My question is, I'm using this beam every day, and it's not broken, nor bend.

It's not broken, but it is bending when loaded.

Why it resist?

Because its strength is adequate to carry the loads.

What is wrong in my calculation?

You are using twice the value of the load F.
Are you applying two loads simultaneously or one at a time?

BA

 

[human909]

2xF is the correct force to use for a impact load, "impacting" from a distance of zero above the object. It is valid for some live loads. No so valid for others.

 

[r13]

We don't have "impact" here. Impact is dynamic in nature, it involves velocity and contact distance. In engineering practice, the dynamic load effect is transformed and expressed as a percentage of the moving weight for ease of calculation, usually less than 1 (100% of the moving object).

During a collision, the impact force can go above 1, when two subjects run into each other with speed, and the deformation (Δ) is very small. The impact force will be infinitely large when Δ approaches zero.

 

[Tomfh]

Retired13,

You’re correct, however some codes use 2F as a simplified way of handling dynamic loading - Eg a beam supporting a lift/elevator.

We structural engineers struggle with dynamics, and the codes often resort to giving us static loads to account for dynamic effects, even though it’s not strictly correct.

 

[r13]

Tomfh,

Thanks for your information. But I would think the use of 2F incorporated safety concerns rather than the true impact effect derived from physics, which happens daily around us, but not well understood, and difficult to evaluate.

 

[m.piron]

After refreshing my memory, I find you was err on equating banana to the orange.

- On the right hand side of your equation, m*g*h is potential energy due to gravity. "h" is the vertical fall distance of an object.
- On the left hand side of your equation, k*x²/2 is energy in linear spring, it can be think as work energy - F*x. "x" is the elongation or shortening of the spring.

I think I am missing something here. By the way, what is the "k" value in your equation?

My assumption is, in the beginning the system have a certain potential energy, when you release the load the beam deflect, and the potential energy is converted into kinetic and elastic energy. When the beam is at the maximum deflection, all the potential energy will be converted into elastic energy, because speed is zero so there is no kinetik energy.

In addition to the likely overestimation of the load, as detailed by others above, realize that the specified yield and ultimate strength are minimums. The actual yield and ultimate are almost certainly higher, probably by at least 10%.

you're right, I look at the properties of that material, UTS=360 MPa is the minimum, but can reach UTS=510 MPa.

there's still something odd about this … does the bar look like it's being stressed to near yield ?

I don't measured it, but looks straight.


Meanwhile, I've done a FEM analysis of that system.

This is the result of the static analysis:

The stress is 224 MPa, the same calculated by hand.
After that, I done a dynamic analysis. In that analysis, I simply placed the load at time 0 (what's happen in reality).
This is the stress over time graph:

As you can see, the maximum stress reached is 350 MPa, 1.6*F. I think that it is less than 2*F due to the damping factor: the potential energy converts into elastic energy and heat due to damping, so the real force is less than calculated.

 

[r13]

Just for fun, let's drop the term "speed (velocity) in the evaluation of impact, and say the impact is due to the transformation of potential energy to work energy, the equation looks like below,

m*g*h = F*Δ, in which h = object travel distance; Δ = elastic deformation of object(s) at contact
Rearrange the terms, we get F = m*g*(h/Δ), and simplified to F = W*(h/Δ)

Example: An object weighted 1 lb, dropped 100" to 3 different mediums below, with the measured settlements 0.1", 1", and 100". What is F for each case?

W = 1 lb , h = 100", Δ = [0.01",1",100"]

1) F = 1*(100/0.01) = 10,000 lbs
2) F = 1*(100/1) = 100 lbs
3) F = 1*(100/100) = 1 lb


What is the results explain to us? Feel free to draw your own conclusion.

 

[r13]

impact is minimum.
If you place a load over a spring, after certain time it stops in the equilibrium position, the travel is x=F/k and the force is F=m*g (I know that "travel" is not the correct term, but I can't translate from the italian "freccia", any help?). But in the beginning, it swing and reach a travel of x=2*F/k. In this condition the load is double the static load.
And the system reach this condition, I can see the beam that swing.
Maybe I must consider it as a static condition, but why?

For a force exerted in motion F = m*a, ie. the pull force on spring.
For a force from fall F = m*g, ie. weight of an object

I hope you can see the difference between the two cases, and apply each thoughtfully.

 

[r13]

The dynamic effect in your analysis is so called "impact", which occurs when both time of contact (duration), and elastic deformation (similar to change in length of spring) at contact approach zero. As pointed out before, impact is dynamic in nature, but simplified to a factor that is used in a static manner for ease of calculation. However, your simple acts on placing and moving object from the beam, in general, will not produce significant dynamic effect to reach the state of 2*F. But you are correct on effects of damping, which can be came from the flexibility of the beam, and rigidity of the supports. This is an interesting topic after all.

 

[canwesteng]

OP is not correct on the effects of damping - it should hardly have any effect on the first sine wave, only reducing the subsequent oscillations.

 

[r13]

Copy from Wikipedia:

A sine wave or sinusoid is a mathematical curve that describes a smooth periodic oscillation. A sine wave is a continuous wave.

The term "damped sine wave" describes all such damped waveforms, whatever their initial phase value. The most common form of damping, and that usually assumed, is exponential damping, in which the outer envelope of the successive peaks is an exponential decay curve.

 

[IRstuff]

> How well does the dynamic simulation match the real motion? You stated that "I simply placed the load at time 0 (what's happen in reality)," but that cannot be if you also say there's no impact, since the instantaneous loading is an impact. If there is no loading, then the motion is some sort of truncated sinusoid, triangular, or exponential, waveform over some finite time, which would greatly reduce the overshoot. The overshoot is greatest with a step function input.

> Materials' specifications are statistical in nature and they are not exact and things don't necessarily fail instantaneously.

https://www.azom.com/article.aspx?ArticleID=6022

states a tensile strength of 360 to 510 MPa. Assuming that your transient is not as severe as you analyzed and the beam is at the high end of its strength, your beam might not have any issue.

TTFN (ta ta for now)
I can do absolutely anything. I'm an expert!

https://www.youtube.com/watch?v=BKorP55Aqvg

faq731-376 forum1529 Entire Forum list

http://www.eng-tips.com/forumlist.cfm

 

[r13]

I think OP meant the object was placed on a softer medium (in practice) as opposed to a stiff medium (in calculation). So the magnitudes of the first sine wave are different, which is caused by the differences in damping property of the materials (some materials capable of absorbing more energy than the others). Otherwise, I agree with canwesteng.

 

[m.piron]

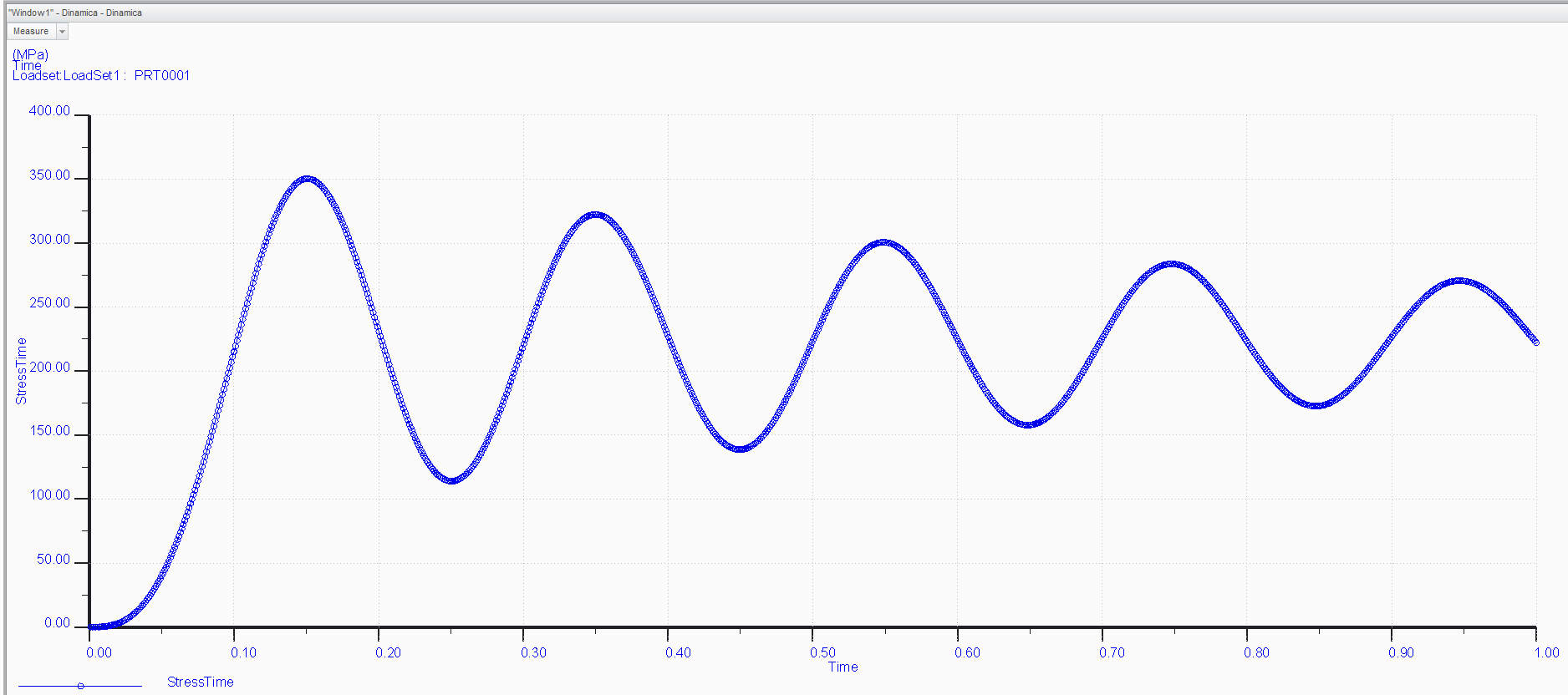
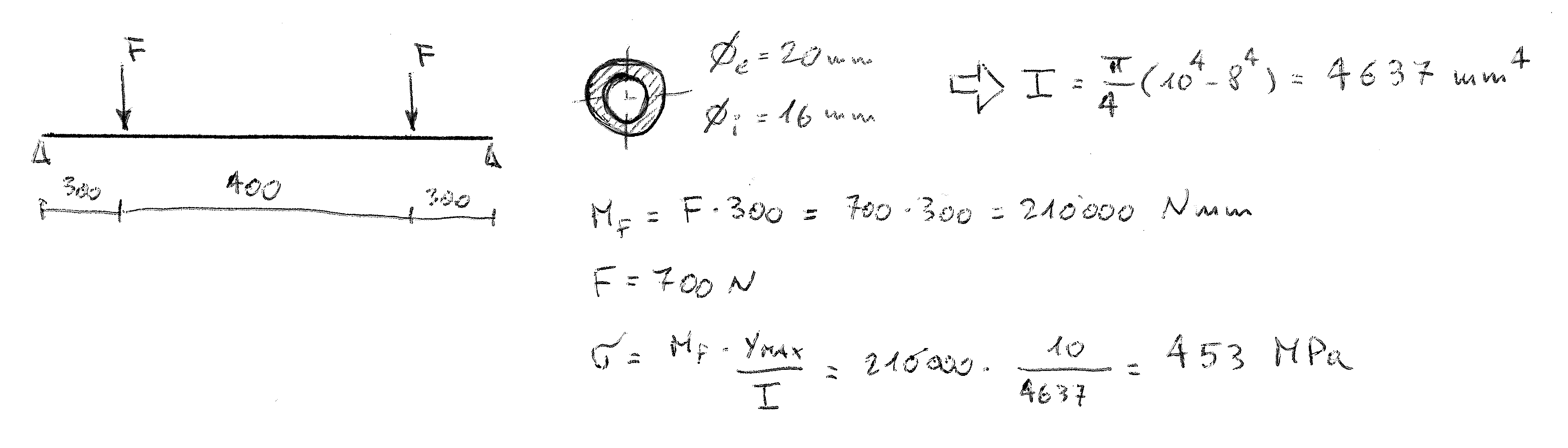OP is not correct on the effects of damping - it should hardly have any effect on the first sine wave, only reducing the subsequent oscillations.

I'm sorry but you're wrong.
Suppose that I'm holding the weight over the beam, the weight touch the beam without load it. In that time, there is no load over the beam: the system have only potential energy.
Then, I release the weight. Part of the potential energy will be converted into elastic energy, the remaining part will be converted into heat (because of dissipation).
It's not simple to calculate by hand, because that part of energy depend on the velocity.

If part of energy will be converted on heat, the deflection of the beam will be less than the deflection calculated without dissipation.
Less deflection = less maximum stress.

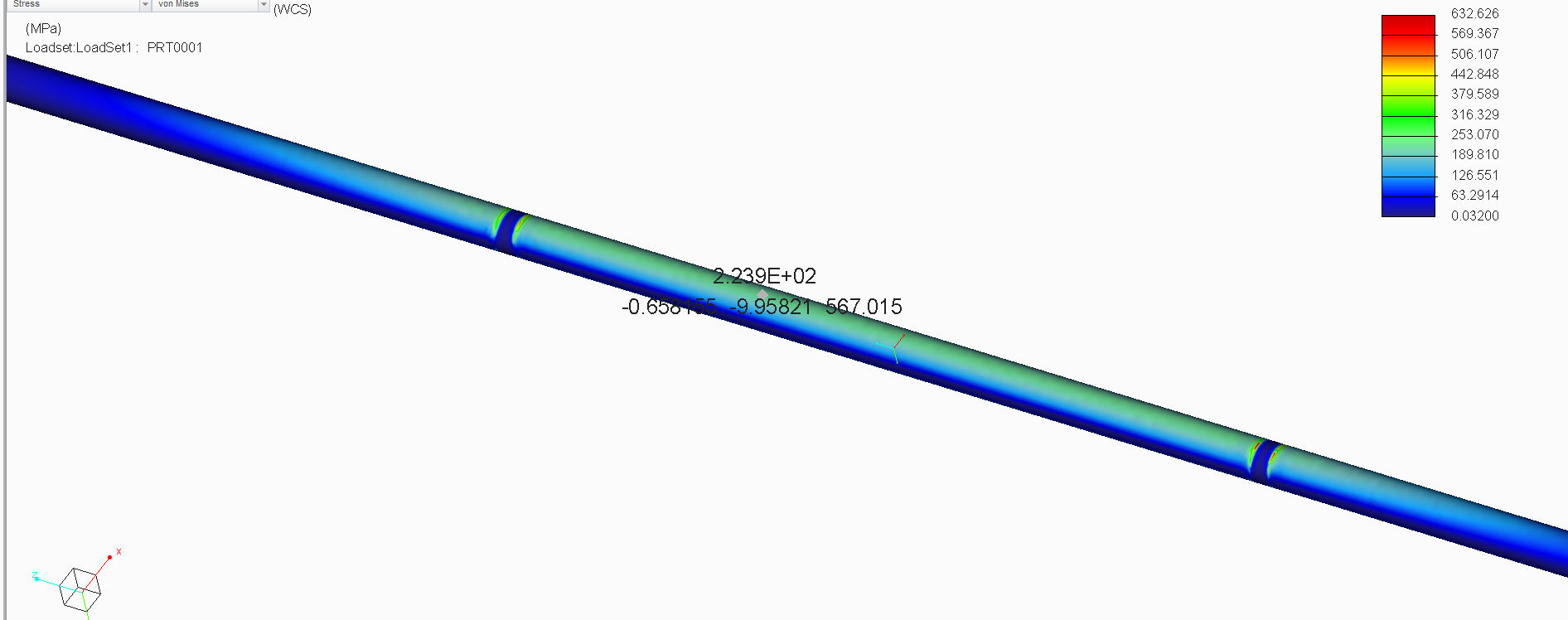
That's why in FEM the maximum stress is 350 MPa, and not 450 MPa as calculated by hand.

I'm pretty sure about that, because I studied a lot car suspension

> How well does the dynamic simulation match the real motion? You stated that "I simply placed the load at time 0 (what's happen in reality)," but that cannot be if you also say there's no impact, since the instantaneous loading is an impact. If there is no loading, then the motion is some sort of truncated sinusoid, triangular, or exponential, waveform over some finite time, which would greatly reduce the overshoot. The overshoot is greatest with a step function input.

> Materials' specifications are statistical in nature and they are not exact and things don't necessarily fail instantaneously.

https://www.azom.com/article.aspx?ArticleID=6022

states a tensile strength of 360 to 510 MPa. Assuming that your transient is not as severe as you analyzed and the beam is at the high end of its strength, your beam might not have any issue.

I don't know how well the simulation match the reality. It's difficult for me to measure it.
The bold part explain why I'm saying there is no impact.
Let me explain with an example: it's not like a car hitting a bumps... it like a car in parking, that you lift (maintaining the contact tire-ground) and then release.
You can't say that this is an impact, but the spring go over the equilibrium point, then rebound, pass throught the equilibrium point, rebound again... (only with old shock adsorber ).
If you want to calculate the torsional stress of the springs wire... is not the stress at equilibrium, but that reached during the rebound, when the deflection is maximum.
And that without impact.

 

[IRstuff]

The issue is the "release;" is it instantaneous or not? If not, then your premise is incorrect. Any other input results in the energy spread out over time; if the spread more than 0.1 seconds, then the overshoot is substantially reduced.

TTFN (ta ta for now)
I can do absolutely anything. I'm an expert!

https://www.youtube.com/watch?v=BKorP55Aqvg

faq731-376 forum1529 Entire Forum list

http://www.eng-tips.com/forumlist.cfm

 

[BridgeSmith]

If the object to be supported is placed, (not dropped) on the pipe you are analyzing (which the previous posts seem to indicate is the case), there is only a small kinetic component to the loading (negligible impact load). In this case, the load on the pipe is only slightly more than the weight of the object, and only for an instant until the pipe stops deflecting.

Rod Smith, P.E., The artist formerly known as HotRod10

 

[canwesteng]

I hope you didn't design car suspensions after all that study then. If you apply a force, F, to a spring, K (or a car suspension), you could have exactly critical damping, and you won't affect the initial displacement at all. Only the rebound effect, or free vibration, will be effected (in this case, this is different for vibrating loads of course, where damping reduces vibration amplitude, but note, that the amplitude of vibrations is always greater than F*k, unless the natural frequency of the spring is smaller than the forcing frequency).

 

[dhengr]

M.piron:
You certainly are making a lot of work out of a pretty straight forward problem. Is this a Ph.D. thesis? Your first calcs., without the load factor of 2 on the loads, does seem to indicate that calcs. indicate/follow reality, as long as they are reality based. You get a bending stress of about 32ksi, likely well within the yield strength of the pipe material, so it continues to function as intended. Unless you are dropping the loads on the pipe beam from some height, or repeating this loading 100 times a day, you don’t have an impact loading or a likely fatigue issue, so give it a rest. You’ll break that pipe quicker by continuing to beat this dead horse, than by the way it is now being loaded. You could strain gage it or actually measure the deflections at several points to help confirm the basic calc. mentioned above.

 

[IRstuff]

If the oscillation exists, it should be readily observable, either visually, or with strain gauge, or with a displacement meter.

TTFN (ta ta for now)
I can do absolutely anything. I'm an expert!

https://www.youtube.com/watch?v=BKorP55Aqvg

faq731-376 forum1529 Entire Forum list

http://www.eng-tips.com/forumlist.cfm