Redacted
Structural
- Mar 12, 2016
- 160
Hi there,
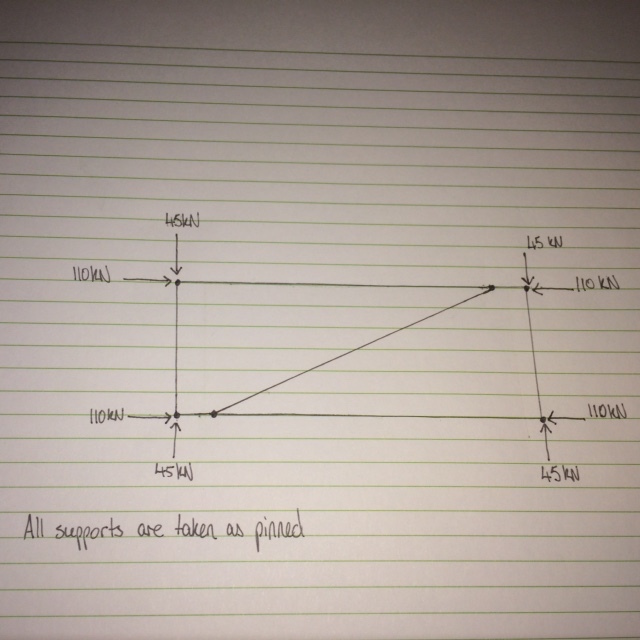
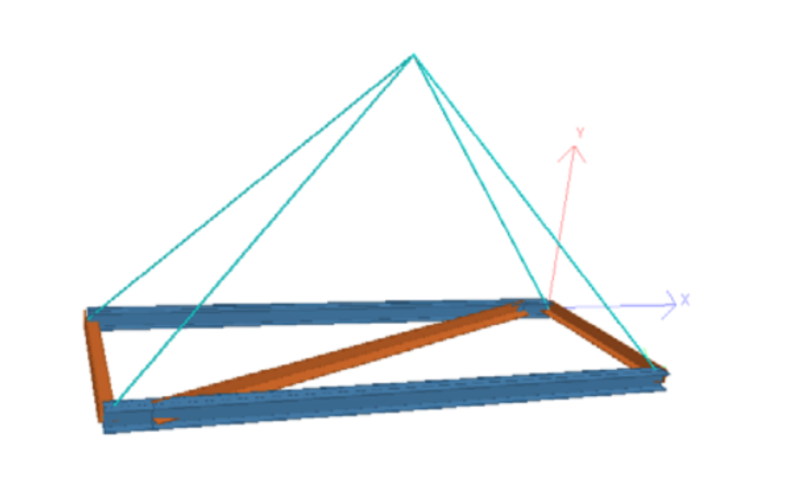
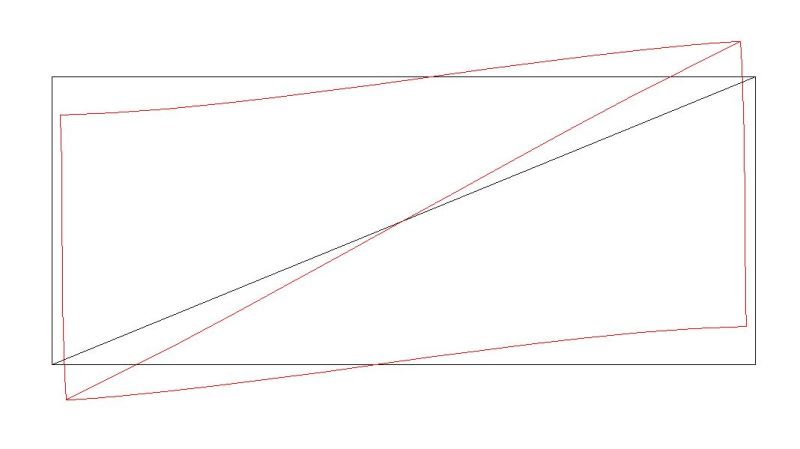
I am trying to determine the axial load in a diagonal brace in a frame. I thought the method to calculate the load would simply be as shown in the attached image, which gives an axial tension load of about 120 kN. However when I modelled the same frame in Staad pro to verify, it only gave me an axial compression force of 0.6 kN for the bracing member. The Staad pro model gave the same results as my hand calculations for the axial compression loads of the external frame members, just not the bracing member, which is why I am a bit confused. Any help would be appreciated.
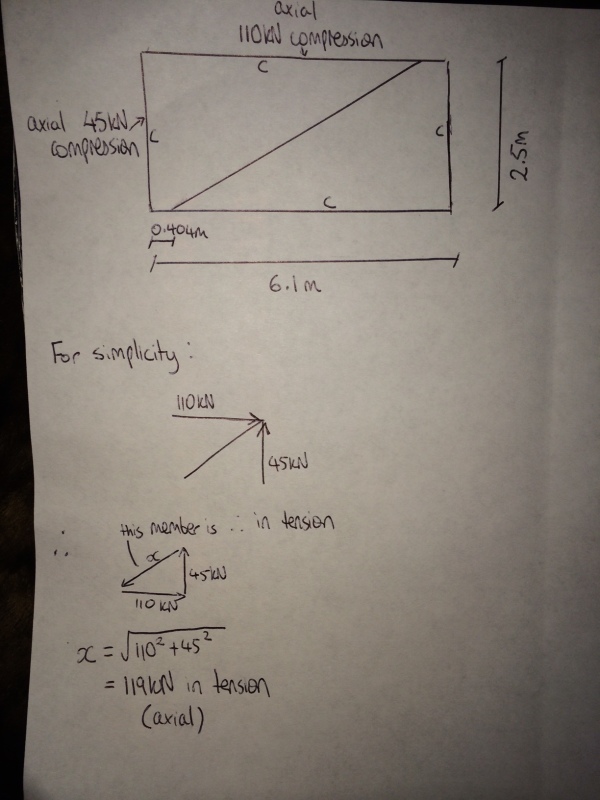
I am trying to determine the axial load in a diagonal brace in a frame. I thought the method to calculate the load would simply be as shown in the attached image, which gives an axial tension load of about 120 kN. However when I modelled the same frame in Staad pro to verify, it only gave me an axial compression force of 0.6 kN for the bracing member. The Staad pro model gave the same results as my hand calculations for the axial compression loads of the external frame members, just not the bracing member, which is why I am a bit confused. Any help would be appreciated.