Often I have to come up with an "effective width" to check a connection capacity. In determining the effective width, I feel like i'm doing just slightly better than just pulling a number out of a hat.
Here's a real application I am working on right now that made me post this:
A lateral load being resisted by a W18 beam's bottom flange.
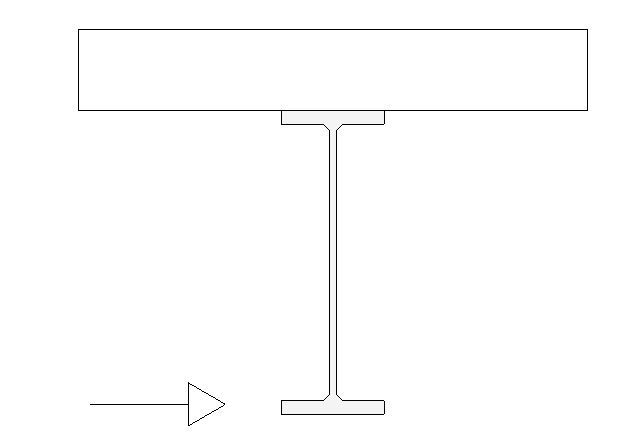
If the load is light enough, I will justify the web resisting the moment (force times 18") in weak-axis bending (section modulus taken as effective width * thickness^2 / 6). Thinking a 1 to 1 force distribution is logical, the effective width would be 18" * 2.
Does this seem practical, and do you guys do the same? Don't want to go too far out on a limb with my "engineering judgement".
Here's a real application I am working on right now that made me post this:
A lateral load being resisted by a W18 beam's bottom flange.

If the load is light enough, I will justify the web resisting the moment (force times 18") in weak-axis bending (section modulus taken as effective width * thickness^2 / 6). Thinking a 1 to 1 force distribution is logical, the effective width would be 18" * 2.
Does this seem practical, and do you guys do the same? Don't want to go too far out on a limb with my "engineering judgement".
