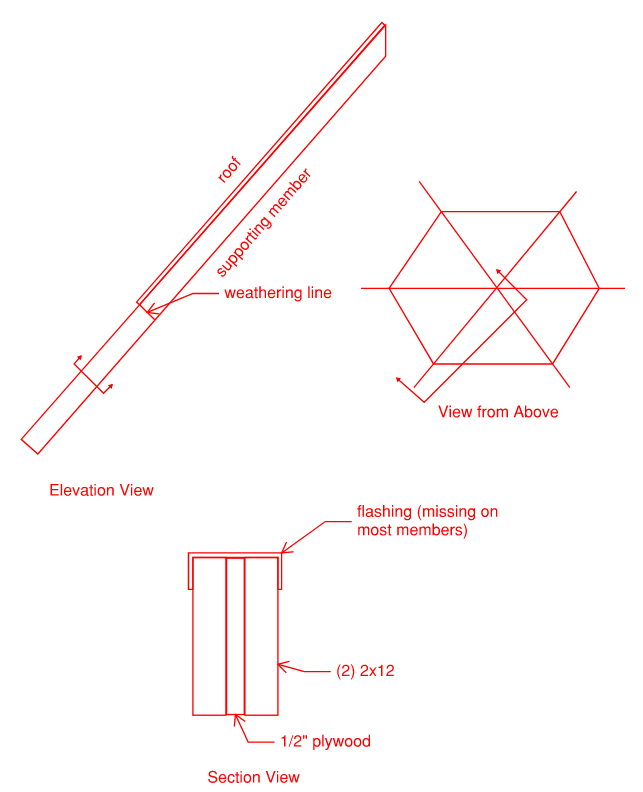
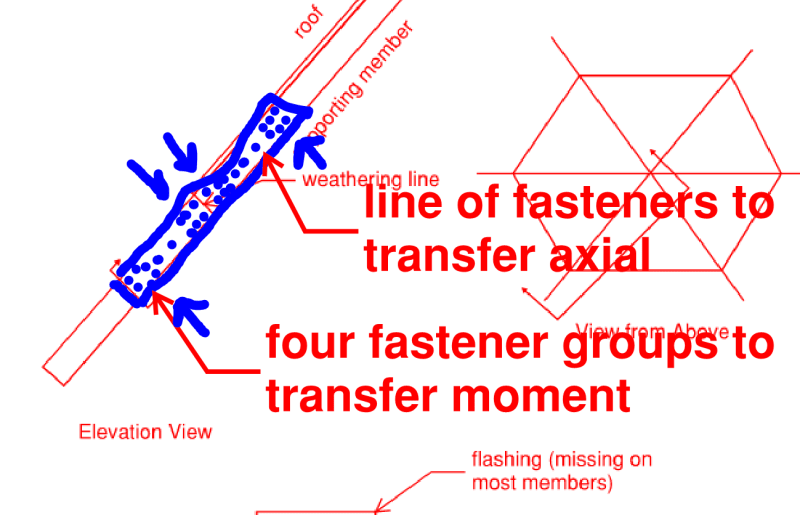
I am currently designing a repair for a wooden structure located in a park. The wooden member being repaired is composed of (2) 2x12 timbers with 1/2" plywood in the middle that has deteriorated due to the flashing coming off and the prolonged exposure to moisture. The repair would replace the bottom section of each member with an equivalent section that is spliced onto the existing. My problem is that I would like to design the splice for the section capacity of the existing to avoid having to do a full analysis of the structure.
I have created a sheet that will calculate all of the dowel yield modes for nearly every connector in the NDS and calculate the LRFD design stresses of the member. The tension, compression, and shear are all very straight-forward, but I am having trouble with the bending. If I use the elastic method and calculate the force based on a moment derived from the F'b x Sx, an equivalent shear at the connection's eccentricity, and the polar moment of inertia, then the shear demand in the bolt is an order of magnitude larger than the design tension & compression and 2 orders larger than the design shear. I tried using the instantaneous center of rotation method based on the fastner's capacity, and although the shear demand is decreased, it still exceeds the capacity of the bolts in the NDS dowel failure modes. If I take the moment calculated from F'b x Sx and divide it by the vertical spacing between the top & bottom bolts, I am getting something much more acceptable that falls below the NDS dowel failure modes, but I understand this method may be unconservative, even though this moment would likely not act in conjunction with another force besides possibly the compression.
Any advice on how to resolve the above issue? I did a preliminary analysis and got a lower bending demand stress, but there's not really a way to take that design stress and use the ICR method with it like I can for the elastic method.
I have created a sheet that will calculate all of the dowel yield modes for nearly every connector in the NDS and calculate the LRFD design stresses of the member. The tension, compression, and shear are all very straight-forward, but I am having trouble with the bending. If I use the elastic method and calculate the force based on a moment derived from the F'b x Sx, an equivalent shear at the connection's eccentricity, and the polar moment of inertia, then the shear demand in the bolt is an order of magnitude larger than the design tension & compression and 2 orders larger than the design shear. I tried using the instantaneous center of rotation method based on the fastner's capacity, and although the shear demand is decreased, it still exceeds the capacity of the bolts in the NDS dowel failure modes. If I take the moment calculated from F'b x Sx and divide it by the vertical spacing between the top & bottom bolts, I am getting something much more acceptable that falls below the NDS dowel failure modes, but I understand this method may be unconservative, even though this moment would likely not act in conjunction with another force besides possibly the compression.
Any advice on how to resolve the above issue? I did a preliminary analysis and got a lower bending demand stress, but there's not really a way to take that design stress and use the ICR method with it like I can for the elastic method.