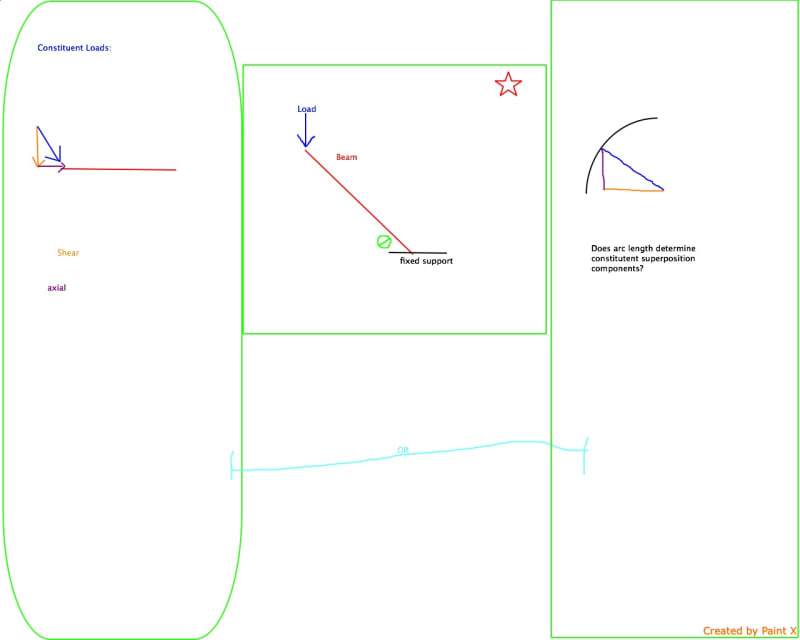
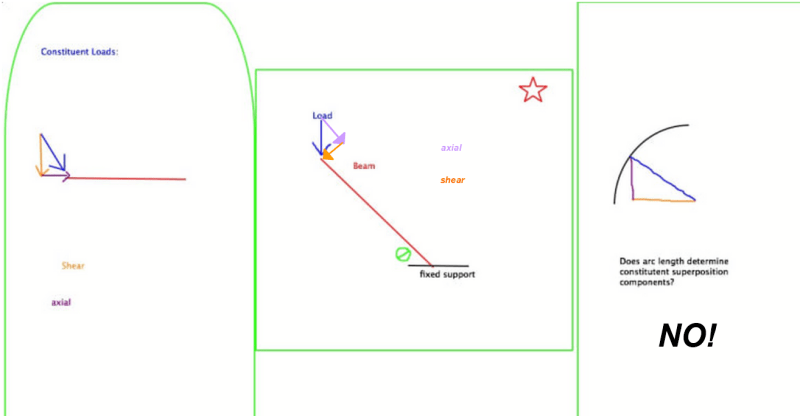
It's interesting to think about - based on my experience from Calc 2 back in the day, the concept of arc length will haunt my dreams forever. However, I don't believe that arc length has much to do with this.
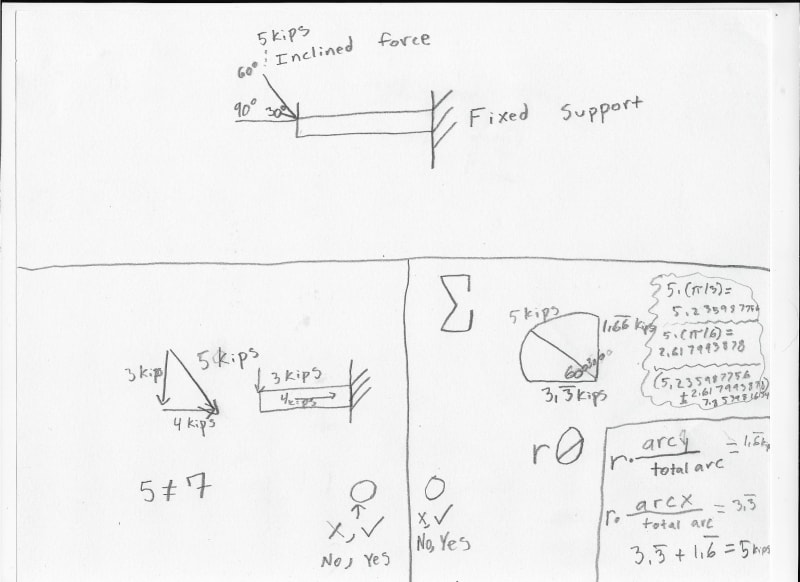
Regardless of where it exists in space, a force is a force. Changing arc length does not increase the magnitude applied force. It's important to note that the reaction moment at the base of the beam will be proportional to the length of the beam though. That is, the longer the cheater bar, the bigger the cheater force. The reaction forces will remain the same though (if your applied force is Fx = 2 kip at 5 ft out or 10 ft out, the reaction force would still be Fx = -2 kip).
I guess what I'm saying is that reaction moment is proportional to length, and arc length is proportional to length, therefore the reaction moment is indirectly proportional to arc length.
Determining the component forces for any given set of axes is a function of the angles that the X and Y (or X' and Y') axes make with respect to the given force. In other words, all you need to do is draw a right triangle where the force vector is the hypotenuse. Then, use trig (remember SohCahToa) and figure out the lengths of sides A and B. Component forces are essentially just projections of vectors onto other sets of axes.