BAGW
Structural
- Jul 15, 2015
- 392
Hi,
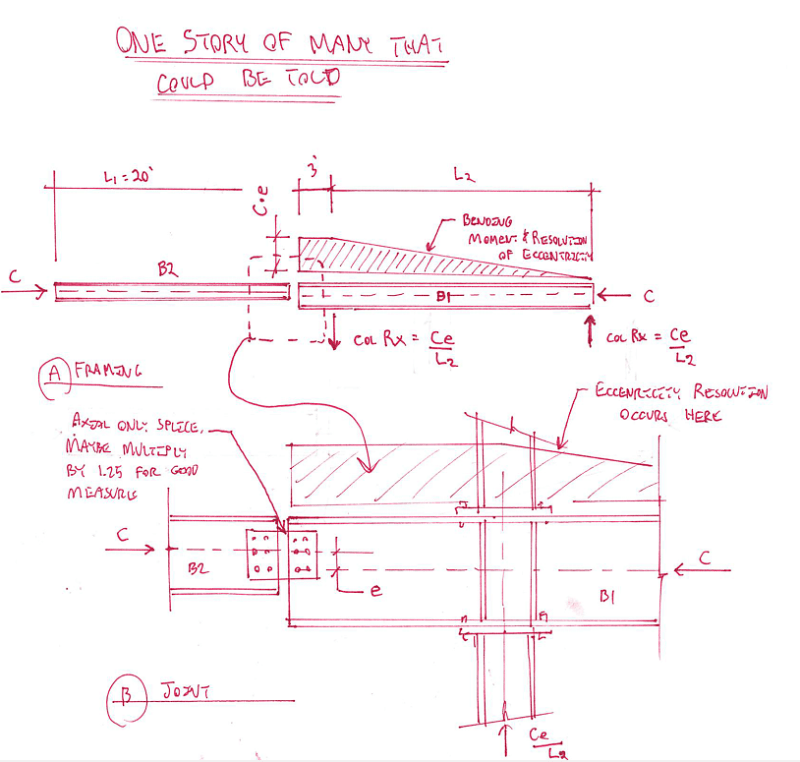
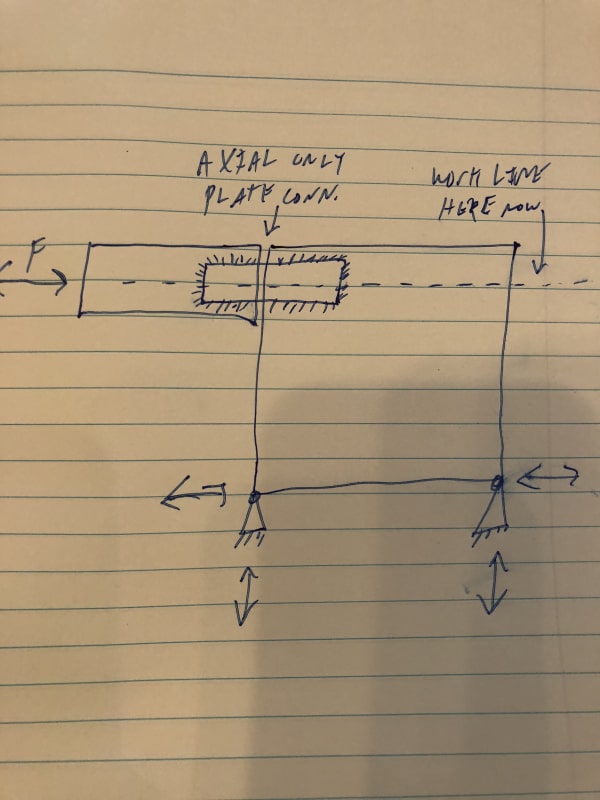
Axial force is transferred from Beam 2 to Beam 1. There is depth difference between Beam 1 and Beam 2 as shown in the image. Connection between beam 1 and beam 2 is web splice plate. There exist eccentricity between beam 1 and beam 2. Work point is at the center of depth of Beam 2. I was told that there are two ways the eccentric moment can be resisted. a) Designing the beam 2 and beam 1 for eccentric moment or b) designing the connection and beam 1 for eccentric moment. Option ‘a’ is something which I am unsure of. Can the beam be designed for eccentric moment and the connection be designed only for axial force? Is this a valid load path?
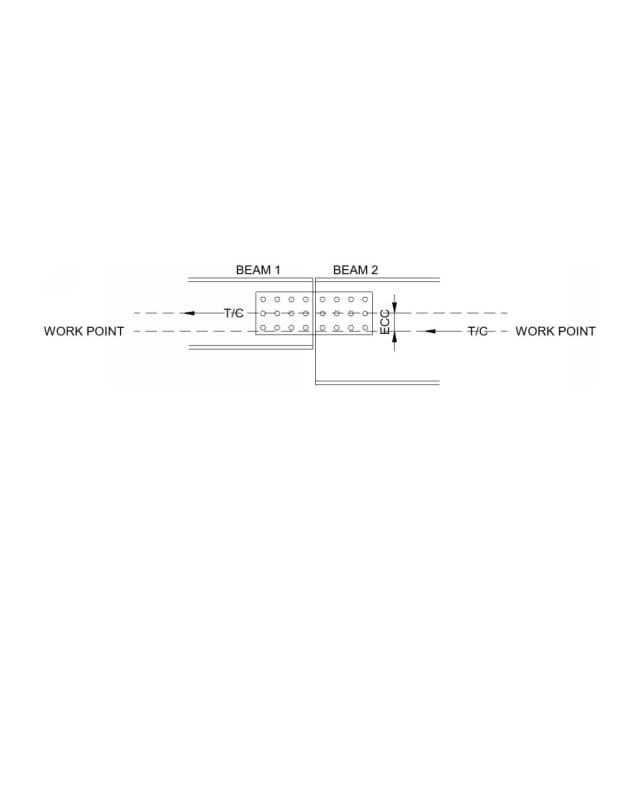
Axial force is transferred from Beam 2 to Beam 1. There is depth difference between Beam 1 and Beam 2 as shown in the image. Connection between beam 1 and beam 2 is web splice plate. There exist eccentricity between beam 1 and beam 2. Work point is at the center of depth of Beam 2. I was told that there are two ways the eccentric moment can be resisted. a) Designing the beam 2 and beam 1 for eccentric moment or b) designing the connection and beam 1 for eccentric moment. Option ‘a’ is something which I am unsure of. Can the beam be designed for eccentric moment and the connection be designed only for axial force? Is this a valid load path?