Concrete compression strain vs inelastic strain

[drennon236]

I have a set of inelastic strains, for which I need to find the corresponding compressive stress. This is the formula I want to use (5.1-26), the encircled strain is defined as "concrete compression strain" in the paper.

.
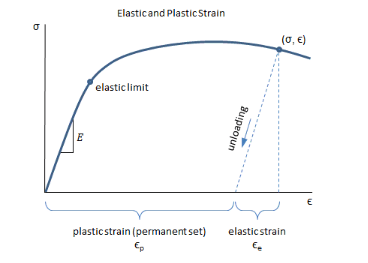
This is definition of strain:

.
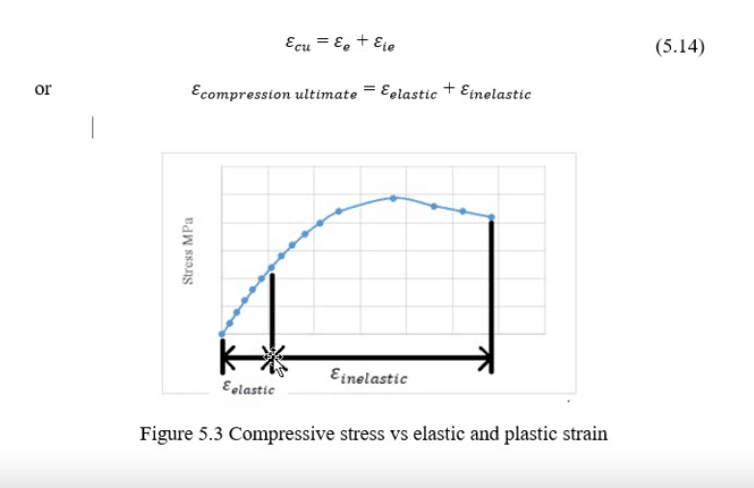So I am wondering if the "concrete compression strain" in the first picture is the same as inelastic strain? - if not what do I have to use as "concrete compression strain"?

 

[IDS]

The concrete strain in the paper is the total strain due to load, i.e. excluding creep and shrinkage strain.

Do you have a definition for your "inelastic strains"?

Doug Jenkins
Interactive Design Services

http://newtonexcelbach.wordpress.com/

 

[Blackstar123]

I think, the strain (circled by you) is the value of strain at which you want to find the stress and thus will be equal to total strain (elastic+inelastic) for a value of ec greater than elastic strain.

 

[drennon236]

Hey IDS, I've attached a picture explaining the definition of inelastic strain.

 

[r13]

[Revised] - Inelastic Strain at Given Stress Level
Chart deleted for mistake

 

[drennon236]

Hey retired13, is then the second picture I posted wrong? Because it seems to contradict your revised picture? - or is there something I am not seeing here. As I understood it, elastic strain was defined as the strain on the x-curve as long as the behavior is elastic, and the inelastic strain is the strain when the concrete starts showing plastic behavior.

 

[IDS]

The stress-strain formula in your original post is an approximation that doesn't have an elastic component. It uses the total strain for all stress levels.

You need to find out what elastic strain was used to determine the inelastic strains you have been given, and add that to give the total strain, which you can then use with the fib formula.

Doug Jenkins
Interactive Design Services

http://newtonexcelbach.wordpress.com/

 

[r13]

This may explain.

 

[r13]

This is an idealized stress strain curve that ignoring the curvatures after the true elastic limit, which usually occurs at a fairly low stress level (0.25 fc' - 0.5 fc'). For this case, the graph indicates the stress strain relationship is linear up to the stress level of 0.9 f_cm, the corresponding strain, therefore, is the elastic strain, and strains beyond that point is inelastic.

Note that elastic strain is recoverable upon unloading (thus the name "elastic"); while inelastic strain is the unrecoverable portion of the total strain.

 

[drennon236]

Thank you retired13, could I also ask you another question. I need to find the cracking strain, and I believe I need to find this from the crack opening (x-axis on the second picture). Is it possible to convert crack opening to cracking strain?

 

[drennon236]

"The cracking strain is defined as the total strain minus the elastic strain "

 

[r13]

Eo is the elastic modulus, and σ_t is concrete rupture stress, per ACI, it is 7.5√fc', and ranged between 5√fc' and 8√fc' from available literatures.

 

[Celt83]

retired13:
I'm not sure that is entirely accurate if Eo is the elastic modulus then I believe σt would be, per ACI Commentary, 0.45f'c which can also vary between 120% to 80% of that value. ASTM C469-02 is referenced by ACI as having methods for establishing the elastic modulus. Although a bit tough to be sure without seeing the full document behind the OP's screenshot.

My Personal Open Source Structural Applications:

https://github.com/buddyd16/Structural-Engineering

Open Source Structural GitHub Group:

https://github.com/open-struct-engineer

 

[r13]

FYI

 

[drennon236]

I am trying to model this theoretical Abaqus concrete damaged plasticity model in tension. I need to model the stress-strain curve after the red line (non-elastic behavior).

This is whats given in FIB code for tension;

Looking at the first picture, the non elastic behavior happens after 0.9*f_ctm - but the slope is positive, the curve keeps increasing while for abaqus after the red line it decreases. For the second picture, this behavior looks more similar to the abaqus model, but the x-curve is not strain, but rather the crack opening in [mm]. Which model from the fib would you say is equivalent to the abaqus model?

 

[r13]

Celt83,

Since the actual stress strain curve is nonlinear, as opposite to the idealized/approximate E, I shall have stated Eo is the "actual elastic modulus" with reference to the very short true elastic range, that starts at zero stress (and zero strain) and ends in between 0.25fc' and 0.45fc' (depends on the strength of the concrete).