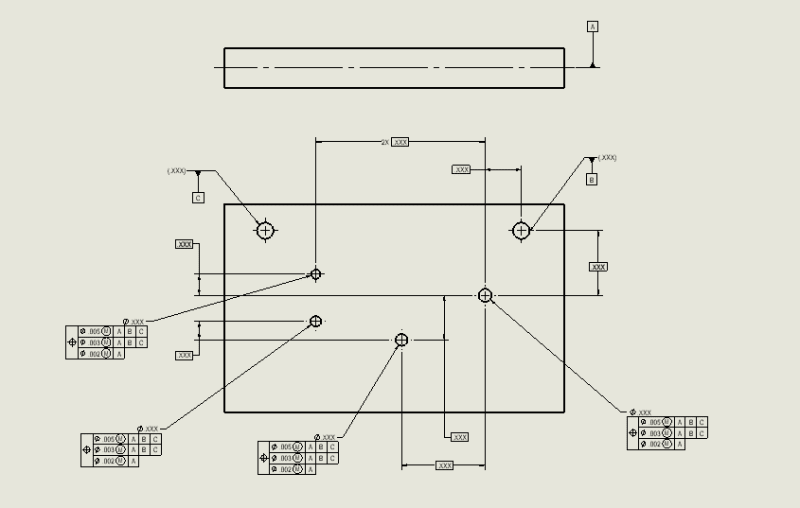
greenimi,
I know the issue that you're referring to here, with the datum features in the 2nd segment that appear to have no effect. I've spent a lot of time studying this, starting more than 10 years ago. You've made my day by asking about it - this gives me the opportunity to shamelessly plug Y14.5.1-2019 Mathematical Definitions of Dimensioning and Tolerancing Principles.
burunduk and pmarc are correct - repeating the A|B|C sequence in the 2nd segment is fine, and that the B and C references actually do affect the constraint. But this would be difficult to conclusively prove using references from Y14.5. There are conflicting explanations in different sections - some are correct, and others are not. One of the main problems has been the interpretation of the following statement from Section 10.5.1 (b):
(2) When datum feature references are specified in a lower segment, the FRTZF is constrained only in rotation relative to the datum reference frame.
The most common interpretation is the one that you arrived at, in which the datum features in the lower segment(s) only constrain rotational DOF's. It follows that if there are no rotational DOF's available that the datum feature is capable of constraining, then that datum feature has no effect. This would be the case for secondary datum feature B in the OP example - datum feature A has already constrained 2 rotations, and B can't constrain the 3rd rotation. Y14.5 actually supports this, in the next paragraph:
When datum feature references are specified, one or more of the datum feature references specified in the upper segment of the frame are repeated, as applicable, and in the same order of precedence, to constrain rotation of the FRTZF. In some instances, the repeated datum feature references may not constrain any degrees of freedom; however, they are necessary to maintain the identical datum reference frame, such as datum feature B in the lower segment in Figure 10-43.
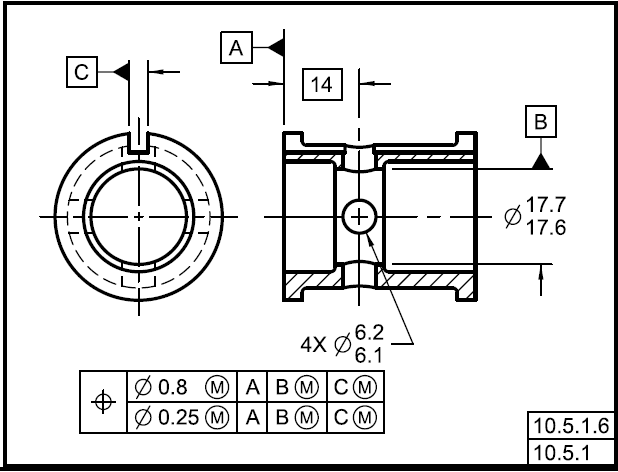
Not only does is seem very strange that there would be spurious "placeholder" symbols, if we follow the logic of the underlined statement it doesn't agree with what is shown in the 10-43 "means this" figure. The caption states that "the FRTZF is constrained in rotation to datum plane A, datum axis B, and datum centerplane C". If the reference to feature B really had no effect, then there wouldn't be a datum axis B. The 3rd rotational DOF would just be constrained by datum centerplane C. In fact, the reference to datum feature B does have an effect.
It turns out that there is another way to interpret "the FRTZF is constrained only in rotation relative to the datum reference frame", which turns out to be the correct one (or, at least, one that makes sense with the figures in Y14.5). The datum features in the lower segment constrain rotational and translational DOF's like they normally would, and then the FRTZF is allowed to translate relative to the DRF. So the "rotation only" effect in the lower segment pertains to the "float" of the tolerance zone framework, not the constraint applied by the datum features. The way I like to describe it is that the lower segment of a composite acts kind of like an orientation tolerance for the pattern.
With this logic in mind, here is the progression of constraint for the second segment in the OP example:
A: Constrains rotations u and v, translation Z
B: Constrains translations X and Y
C: Constrains rotation w
Translations are then "floated" for the FRTZF. So both B and C participate in the w rotation - B provides the "pivot axis" and C provides the clocking.
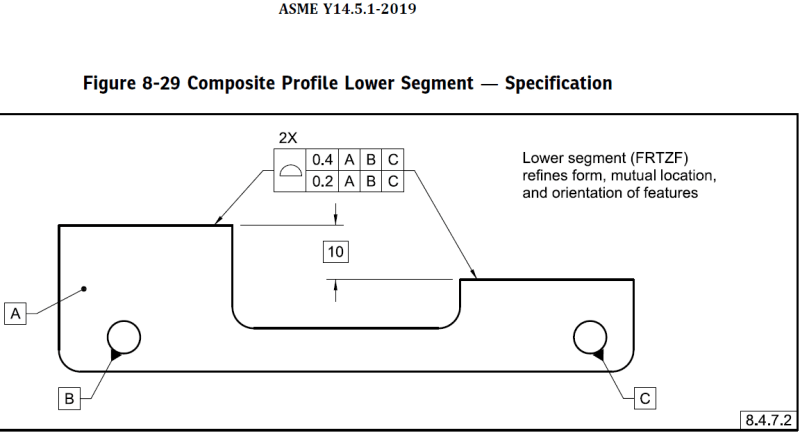
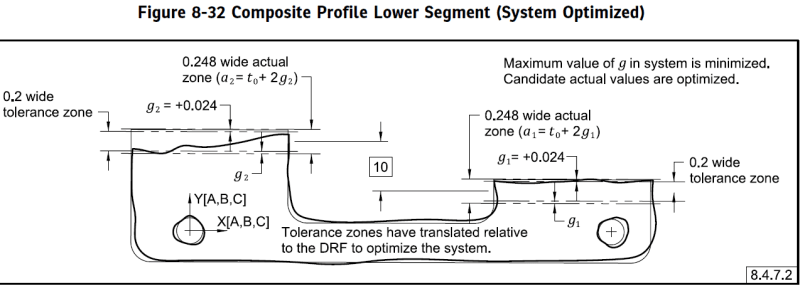
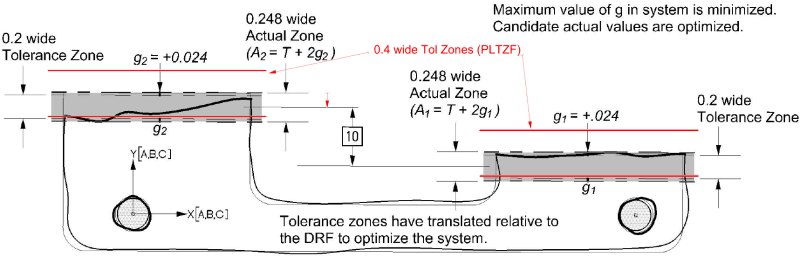
I'm proud to say that we addressed this particular case in Y14.5.1-2019. I included an example in the profile section, that has a composite profile tolerance with a datum feature configuration identical to the OP example. Here are the relevant figures, that show the drawing spec and the final optimized system:
Note that because of the A|B|C sequence, B defines the XY origin and C defines the w rotation of the X axis. The B simulator expands fully, and then the C simulator expands. If the sequence was A|B-C|, then the B and C simulators would expand simultaneously and constrain the X, Y, and w DOF's together. The resulting DRF would be slightly different in this case.
Evan Janeshewski
Axymetrix Quality Engineering Inc.