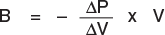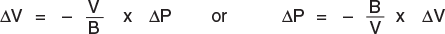closed room emptying 1

[gtsolid]

Good morning,
I have a fixed volume room under oil pressure. In 1 night i notice that the pressure lowers of 10%.
Can i conclude, since the oil is incompressible, that the quantity of oil remained is 10% less?
Reasoning i think it's not possible, because if i lose 0.1l of oil i think the pressure goes to 0. How can i calculate this quantity?

 

[LittleInch]

You need to define your issue a bit more and a sketch always helps.

Are you talking about a fixed volume sealed inside some rigid container under pressure?

Looks like thermal contraction to me. Oil is very susceptible to thermal effects on expansion and contraction.

There is an FAQ on this here:

https://www.eng-tips.com/faqs.cfm?fid=1339

Remember - More details = better answers
Also: If you get a response it's polite to respond to it.

 

[gtsolid]

Hi,
yeah, the concept is that, here a sketch:

i let the oil come inside, at 50bar, then i close the tap (in the reality the tap is before the gauge) and let for the night.
In the morning i register the variation.
Surely the oil is very susceptible to thermal effects, but if i consider T=k, how can i study the leakage?

 

[bimr]

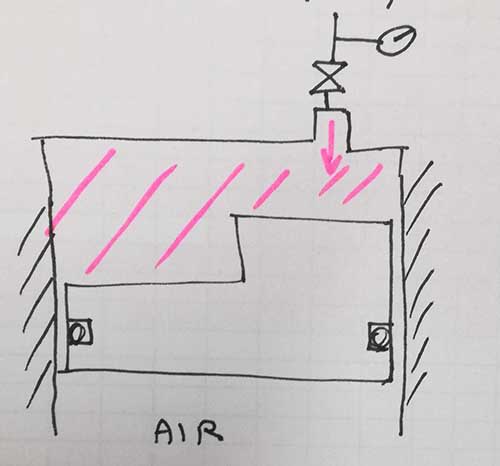
I have a fixed volume room under oil pressure. In 1 night i notice that the pressure lowers of 10%.
Can i conclude, since the oil is incompressible, that the quantity of oil remained is 10% less?

No, the change in oil volume will not be 10% less, but much smaller. There is actually no such thing as an incompressible fluid; the term is just used as a simplification for fluids that are hard to compress. For example, fluids like water and oil are compressible, but it takes such a massive pressure to change the density so that in most cases incompressibility is assumed to simplify hydraulic calculations.

To solve your problem, you have to calculate the compressibility of the oil.

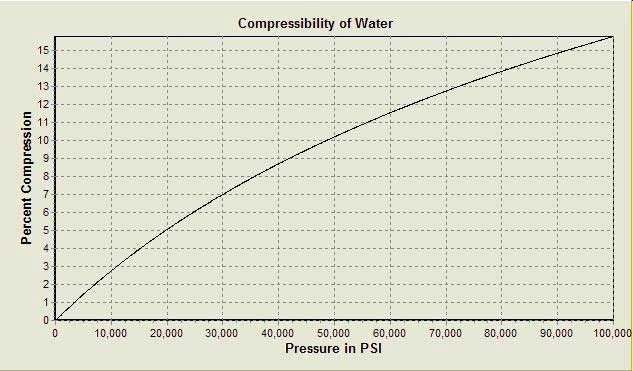
Here is an example, a graph showing the compressibility of a fluid (Compressibility of Water):

In order to calculate the reduction in volume for your oil problem, you have to know the Bulk Modulus of the fluid. The Bulk Modulus is a measure of the resistance of a fluid to compression. It is defined as the ratio of pressure stress to volume.

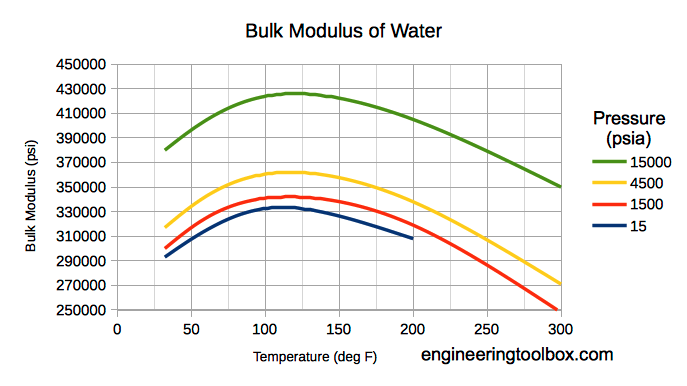
Note that the B (Bulk Modulus) must be corrected for the temperature, pressure of the fluid, and the amount of entrained air. The following graph shows how temperature and pressure affect the Bulk Modulus of a fluid (Water):

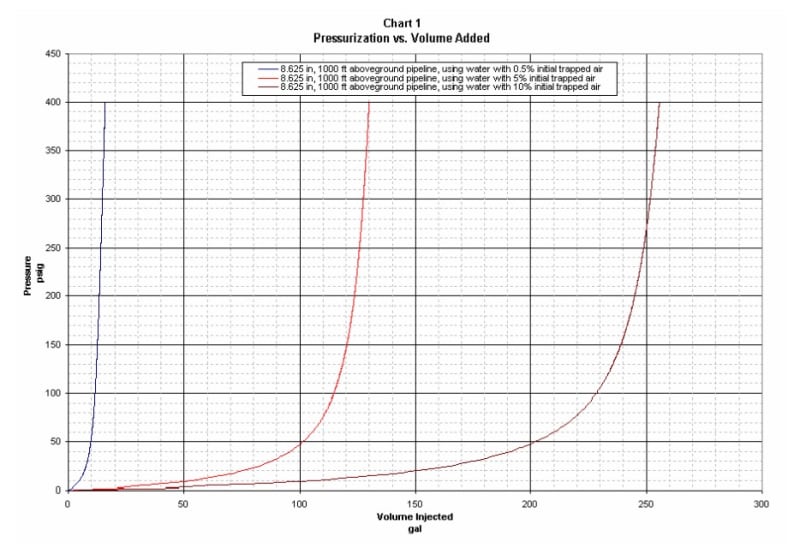
For a real life example, the image below indicates the additional amount of water that is necessary to increase the pressure of a filled pipeline when conducting hydrostatic testing.

To calculate the volume change for your oil problem, you need to know the bulk modulus of oil and then apply it using the simple formula below,

As an example:

MIL-H-83282 oil has a bulk modulus of 3.0 x 10⁵ psi. Thus, a pressure increase of 3000 psi will reduce its volume by 1.0%.

When the value of the Bulk Modulus is known, it is simple to calculate the effect of any pressure change on volume, or of any volume change on pressure.

In a real application, the bulk modulus has to be modified for the working pressure, actual temperature and percent of entrained air.

The actual bulk modulus B = EP x ET x EA x Bref, where Bref = Tangent adiabatic bulk modulus psi stated at 100°F, 2500 psi and no entrained air (A reference point).

Link to reference

 

[racookpe1978]

bimr:
Your post is excellent, but he'd have change those graphs from water constants to nominal oil constants for that temperature, right?

Can't figure out why his sketch assumes T = constant overnight.

 

[bimr]

Thanks, you are correct. Seems that I lost my train of thought in the middle of the answer. If I have time later, I will fix it.

 

[gtsolid]

I assume T=k for the case in which i have to consider a short time situation, not the other one. In this case i want to calculate the mass lost for leakage
@bimr: good post! but my V=k (it's a cylinder under pressure≠k, p changes during the night because of T)

 

[LittleInch]

gtsolid,

your sketch is better but it's now far from clear what is going on at the bottom of the movable piston (i.e. finish off the sketch...)

Is pressure of air the same as that of the oil?
What stops the air from leaking out?
Where are the potential leak paths?
How do you know that the valve isn't leaking?

What else aren't you telling us?

Remember - More details = better answers
Also: If you get a response it's polite to respond to it.

 

[gtsolid]

Now i'm able to calculate the Δp caused by ΔT.
But if T=k, how can i calculate the mass lost in order to have the same Δp as above?

 

[bimr]

gtsolid, look through my edited post. There is an adjustment to the Bulk Modulus for temperature change.

 

[gtsolid]

I'm OK with ΔT (a delta of 10°C for example produces a Δp of x bar...), i'm focusing on Δm now.
Maybe i can use the first principle for open system?

 

[racookpe1978]

No. If you have any change in mass allowed, then ALL assumptions of a simple "delta T => delta Pressure" must be re-evalutated.

You still have not explained the basic geometry of the problem, and the basic process going on.

 

[KevinNZ]

The mostly cause of pressure change is the air space below the piston. The air pressure is the same as the oil pressure. If not the piston moves. Small change in temperature will have large effect on the air pressure and thus the oil pressure.

 

[LittleInch]

Kevin, We don't know what is below the piston because the OP hasn't told us...

Also effect of temp on air is much less than the liquid oil because it's compressible and the temperature difference is based on degrees K, not C, so a 20C temp difference isn't that much when its say 303K to 283K

Also I think T=k is some sort of shorthand for temp is constant.

Remember - More details = better answers
Also: If you get a response it's polite to respond to it.

 

[gtsolid]

Hi guys,
My application is of this kind:

i have leakage and i have to investigate.
In orange the piston, circled in blue the standard volumes filled by oil.
If a seal is damaged (red body), the upper chamber (in black) can be in contact with the sensor one (surface in light blue). And my component is full of oil.
it's a double effect piston, as you can see. I wish to compare the change in pressure due to temperature change and due to seal malfunctioning.
5 bar in one night i think is caused by T. This in static condition, because when i start to cycle, i have a lot of leakage...