Calculation of neutral axis of double reinforced concrete section for flexural analysis. 2

[yoohooos]

In Wight's textbook(attached below), presented an iteration method. In which the final answer from this method won't be exact, unless the stepping size is infinitesimally small. Whether the compression steel is yielded or not, it will be determined and accounted during this process, but still, the final answer won't be exact.

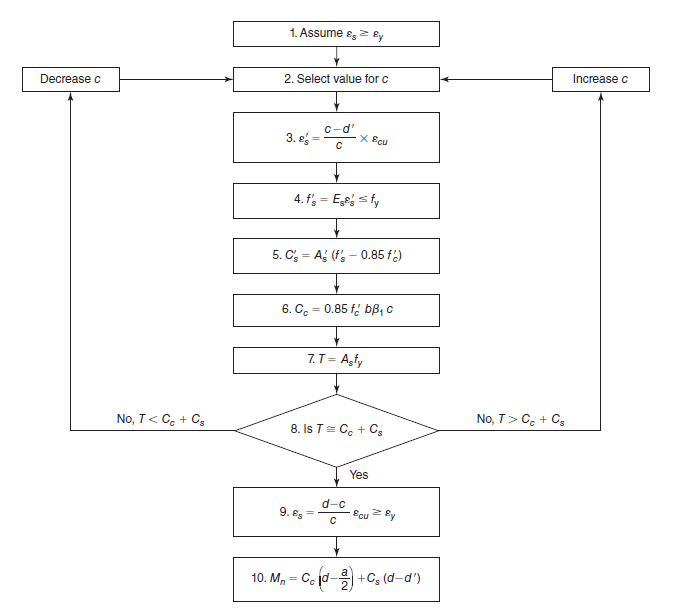
Instead of using this method, would it be better to just solve for the neutral axis directly from the equation?
Assuming tension steel is yielded.
T = C
T = C_c+C_s
A_s*f_y = α₁*f'_c*b*β₁*c+A'_s*(f_y-α₁*f'_c)

​

in case compression steel is yielded
A_s*f_y = α₁*f'_c*b*β₁*c+A'_s*(E_s*(c-d')*ε_cu/c-α₁*f'_c)

​

in case compression steel is not yielded

In which, we can determine which is the correct answer by finding the strain of the compression steel using:
ε'_s = (c-d')*ε_cu/c
and if the ε's matches the condition of that equation, that c is the correct c. With this method, the final solution will be exact, it might not matter much but I think it's still better than near-exact solution.
If this method is incorrect or the assumption is incorrect. Please let me know.

Thank you very much!

 

[Celt83]

Implementing the sudo code from Wright requires you to pick an appropriate method to "increase or decrease" c you can do a constant step size but included a conditional to half the step if within a certain tolerance. Really you are looking for a root to the equation 0=T+Cc+Cs where T,Cc,Cs are functions of c. There are various methods to go about finding that root for a concrete beam the problem domain is very well defined and a solution, if one exists, for the neutral axis is within a range of c=0 to c=1.85*H (if using the whitney block), some methods include Bisection Method, Regula Falsi, Newtons Method, Secant Method, Brent's Method.

Your derived exact formula would only hold true for a rectangular section with a singular layer of top and bottom reinf. where the sudo code presented by Wright could be expanded to cover more general cases.

User IDS has some spreadsheet that I believe use Brent's Method: Link
I've got a sheet that does Bisection, Newton Raphson, A Method outlined by Davister in a paper on computer aided design of concrete cross sections, and Brent's Method: Link

All of these methods will be limited to machine tolerance though so may never actual yield 0 but some very small value or pre-determined tolerance deemed close enough the real root.

Edit: I should mention IDS does have a paper where they do derive a closed form solution for the neutral axis depth slicing the section into trapezoids so it is possible.

My Personal Open Source Structural Applications:

https://github.com/buddyd16/Structural-Engineering

Open Source Structural GitHub Group:

https://github.com/open-struct-engineer

 

[IDS]

Further to the comments from Celt83:

Note that iterative solutions such as Newton's or Brent's methods can be set to converge to any precision you want, subject to machine precision, and the highest precision is 12-13 orders of magnitude more than anything achievable in practice (given unknowns such as the actual Young's Modulus and yield stress and strain of the concrete, and the actual precise position of the reinforcement).

Having said that, the basic closed form solution is fairly simple, even when applied axial load is included, and can be extended to cover almost all sections used in practice, including multiple layers of reinforcement, and any cross section divided into trapezoidal layers. Most of my spreadsheets actually use a closed form solution, and derivation of the formulas for the more complex cases can be found at:

https://newtonexcelbach.com/2008/10/23/reinforced-concrete-section-analysis-6-ultimate-limit-state/

and

https://newtonexcelbach.files.wordpress.com/2008/10/ultimate-moment-capacity1.pdf

The first link above is the last of a 6 post series, also looking at sections within the elastic range, starting at:

https://newtonexcelbach.com/2008/03/25/reinforced-concrete-section-analysis-1/

Sections where the closed form solution is not so easily used include:
- Use of non-rectangular stress blocks, especially those with non-integer exponents over the "parabolic" range, as specified in Eurocode 2 for high strength concrete. However note that for a rectangular section a parabolic-linear stress block can be converted to a rectangular block, that will give exactly the same results.
- For circular sections it is much easier to specify the shape as a single radius, rather than splitting it into multiple trapezoidal layers, and an iterative solution using the exact area for a circular segment will give a more precise result that the closed form solution using a circle approximated with multiple trapezoidal layers.

Finally, for the case in the original post including compression reinforcement, for greater precision deduct the concrete stress from the steel stress in the compression zone (because the steel is displacing the concrete). Formulas with that correction are given in the paper linked in the second link above.




Doug Jenkins
Interactive Design Services

http://newtonexcelbach.wordpress.com/

 

[Guest090822]

Isn’t this just “strain compatibility” which just about every college textbook talks about?

 

[IDS]

Isn’t this just “strain compatibility” which just about every college textbook talks about?

But just about every college textbook suggests an iterative solution, which really isn't necessary in most cases.

Doug Jenkins
Interactive Design Services

http://newtonexcelbach.wordpress.com/

 

[JoshPlumSE]

There are quicker ways to get to the right answer when you're doing a hand calculation. No doubt about that in my mind. The nice thing about a "simple" algorithm like this is that it can't really go wrong. It's very generalized and will work for cases that are more complex (non-rectangular beams, odd reinforcement layouts, etc).

I'm certain that there are better, quicker algorithms out there. The question I have that few people ask is whether the increase in speed is worth it? Let's say this requires 100 iterations per beam. How long does that take?

The answer is different when you are writing the first version of an in-house program that is limited to just a few members, right? If you're working on a commercial program (say RISA or SAP2000) where you may have a model with 100,000 concrete members, then optimizing that routine is probably more important.

 

[Guest090822]

IDS - It depends on the number of layers of reinforcement. If doing this type of analysis for one row of tensile bars and one row of compression bars I’d fire the engineer for wasting time LOL!

 

[IDS]

But just about every college textbook suggests an iterative solution, which really isn't necessary in most cases.

To be fair to college textbooks everywhere, the ones I checked do give the quadratic solution to the ULS bending capacity with rectangular stress block and rectangular section (although they also give the iterative method and more simplified approximate methods).

It is the linear elastic analysis with combined bending and axial load where the closed form solution requires a cubic equation that is invariably solved with an iterative method.

I still think it makes sense to use the closed form solution when doing a computer analysis (with any number of rows of reinforcement), but I agree there is nothing wrong with an iterative solution.

Doug Jenkins
Interactive Design Services

http://newtonexcelbach.wordpress.com/

 

[Ron]

Trying to get overly precise with this exercise is a bit like measuring with a micrometer, marking with a crayon and cutting with an axe.

 

[Guest090822]

Just keep in mind that these same college textbooks also note that accounting for compression bars rarely increases your moment capacity by more than a few percent. Of course, you have to design a few dozen like I did to prove that the textbooks were correct. It's a great academic exercise but that's about it!

 

[JoshPlumSE]

Trying to get overly precise with this exercise is a bit like measuring with a micrometer, marking with a crayon and cutting with an axe.

I have to remember that quote. It is excellent!

 

[IDS]

I think we are all agreed that "measuring with a micrometer, marking with a crayon and cutting with an axe" is not a good idea.

However in this case, since the proposed arithmetic method is both quicker and simpler than iteration, a closer analogy would be trimming paper with a guillotine, rather than a pair of scissors.

You can do an OK job with a pair of scissors, but if you have a guillotine handy it will be easier and quicker, and incidentally give a more precise result.

And if you have to cut hundreds of sheets, there is no argument which is better.



Doug Jenkins
Interactive Design Services

http://newtonexcelbach.wordpress.com/