Hi all,
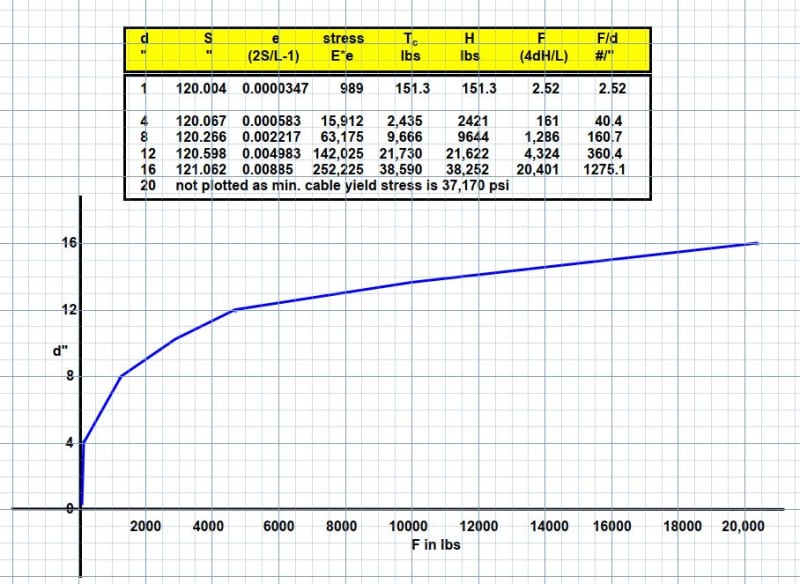
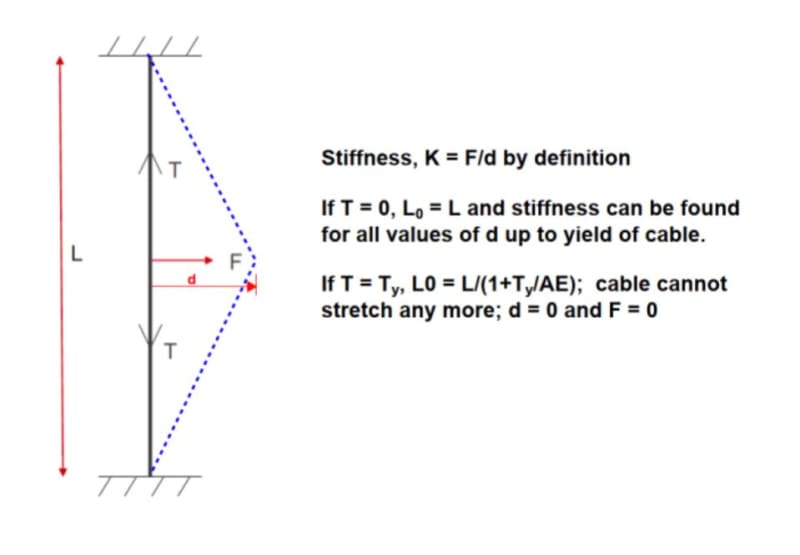
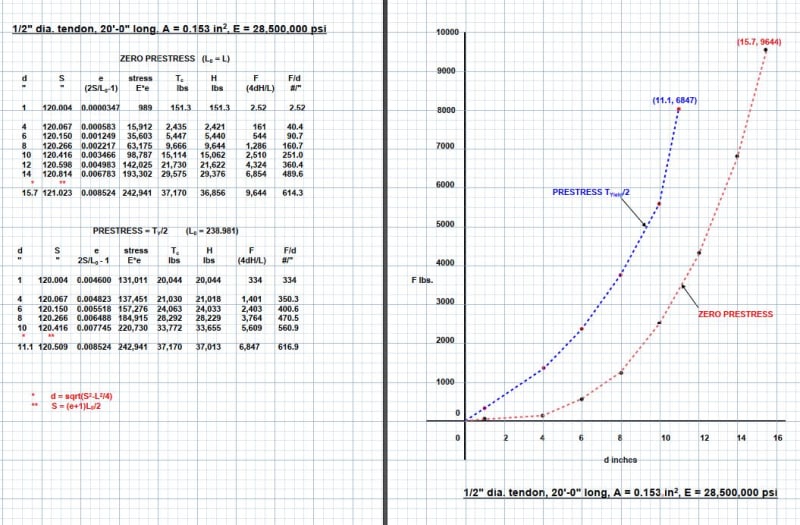
I have a vertical cable of length L that has a pretension T, that is applied a horizontal force at its midpoint. I also know the cross-sectional area A, and I can assume small angle approximations.
How can I compute the stiffness in the horizontal direction? I guess I need to have something like F = K*delta, where delta is the horizontal displacement of the midpoint, but I don't know how to approach it.
Thanks.
I have a vertical cable of length L that has a pretension T, that is applied a horizontal force at its midpoint. I also know the cross-sectional area A, and I can assume small angle approximations.
How can I compute the stiffness in the horizontal direction? I guess I need to have something like F = K*delta, where delta is the horizontal displacement of the midpoint, but I don't know how to approach it.
Thanks.