Hi all.
I did a couple of quick calcs to better understand the phenomenon of biaxial bending. One thing that is currently tripping me up is the sign convention. For example, if we have a rectangular beam as follows
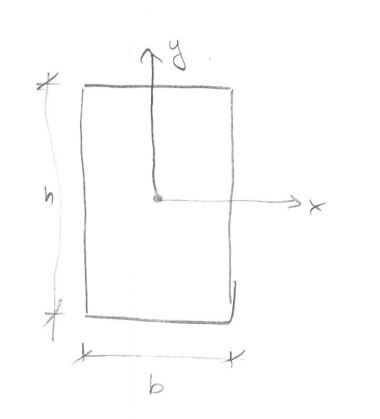
with b = 15" and h = 30" and a coordinate system established as show with origin at exactly the middle. Ix = 33750 in2 and Iy = 8437.5 in2. Furthermore we have a moment Mx of 100 lb.in occuring about the +x axis and a moment My of 100 lb.in occuring about the +y axis. Intuitively, we can tell Mx is causing compression at the bottom and tension at the top of this section. Likewise we can also say My is causing compression at the right and tension at the left of the section. However, when we run the numbers:
sigma_top = Mx*y/Ix = (100 lb.in)*(15 in)/33750 in4 = 0.044 psi
sigma_bot = Mx*y/Ix = (100 lb.in)*(-15 in)/33750 in4 = -0.044 psi
sigma_right = My*x/Iy = (100 lb.in)*(7.5 in)/8437.5 in4 = 0.088 psi
sigma_left = My*x/Iy = (100 lb.in)*(-7.5 in)/8437.5 in4 = -0.088 psi
It is highly confusing to me that sigma_bot and sigma_right, which are both in compression, have opposing signs. Equally confusing is the fact that sigma_top and sigma_left, which are both in tension, have opposing signs. Can anyone bring light to this basic mechanics of materials issue? thanks
I did a couple of quick calcs to better understand the phenomenon of biaxial bending. One thing that is currently tripping me up is the sign convention. For example, if we have a rectangular beam as follows

with b = 15" and h = 30" and a coordinate system established as show with origin at exactly the middle. Ix = 33750 in2 and Iy = 8437.5 in2. Furthermore we have a moment Mx of 100 lb.in occuring about the +x axis and a moment My of 100 lb.in occuring about the +y axis. Intuitively, we can tell Mx is causing compression at the bottom and tension at the top of this section. Likewise we can also say My is causing compression at the right and tension at the left of the section. However, when we run the numbers:
sigma_top = Mx*y/Ix = (100 lb.in)*(15 in)/33750 in4 = 0.044 psi
sigma_bot = Mx*y/Ix = (100 lb.in)*(-15 in)/33750 in4 = -0.044 psi
sigma_right = My*x/Iy = (100 lb.in)*(7.5 in)/8437.5 in4 = 0.088 psi
sigma_left = My*x/Iy = (100 lb.in)*(-7.5 in)/8437.5 in4 = -0.088 psi
It is highly confusing to me that sigma_bot and sigma_right, which are both in compression, have opposing signs. Equally confusing is the fact that sigma_top and sigma_left, which are both in tension, have opposing signs. Can anyone bring light to this basic mechanics of materials issue? thanks
