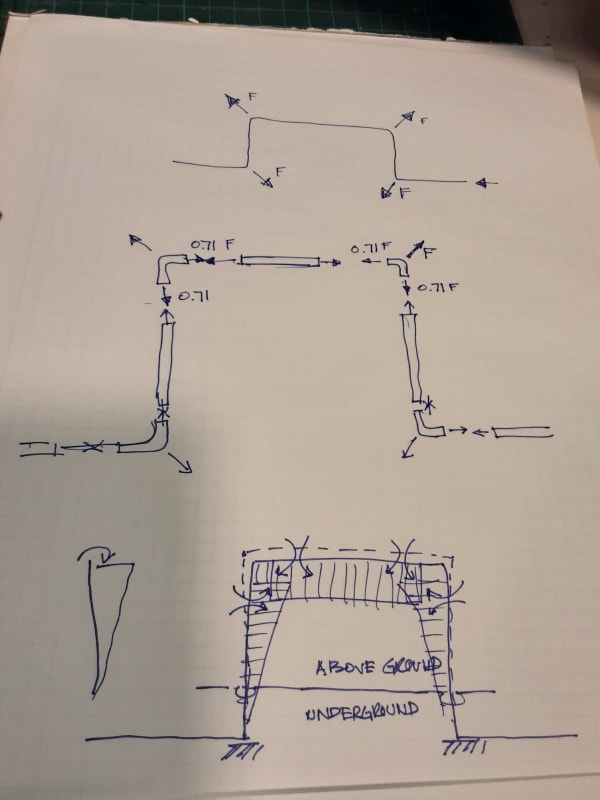
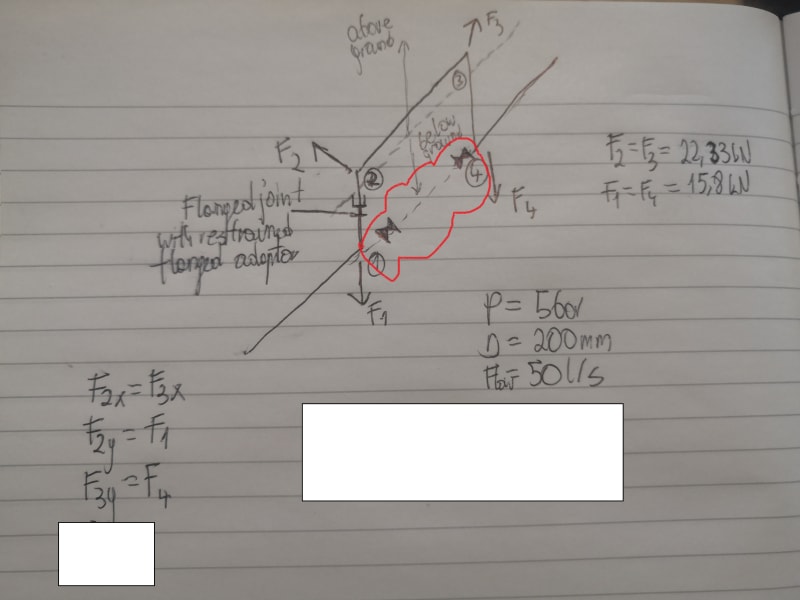
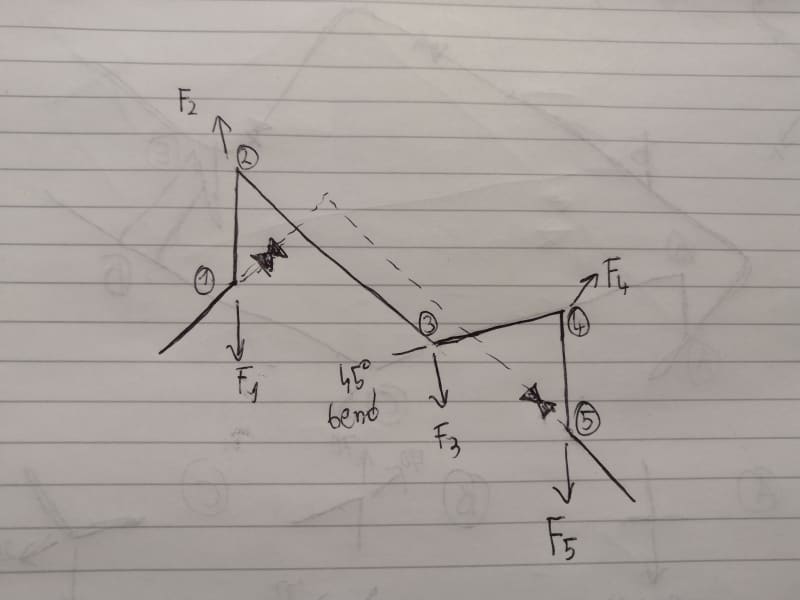
First, momentum forces are generated by flowing mass changing direction at elbows. There are no momentum forces in straight pipe between elbows, because there is no change of the mass x velocity vectors. So all momentum forces are placed at joints only. Since axial force in a pipe can be resisted by both tension and compression in the pipe wall as needed, an axial force placed at the middle of pipe 2-3 in the direction of 2 to 3, half will be transferred to j2 by pipe tension and the other half to j3 by pipe compression. To be more accurate, the distribution to each joint should be adjusted, depending on distance from load to each joint. A load placed at 1/4 pipe length from j2 should have 75% of that force transferred to j2 and 25% transferred to j3.
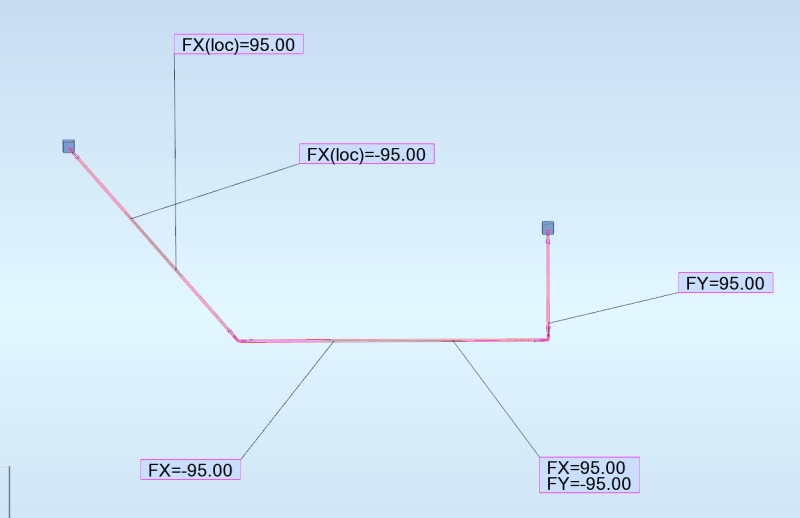
You can also have unbalanced pressure forces generated at elbows. Pressure force = pipe pressure x area of pipe. 10 psi pipe pressure in a pipe with 100 in2 of internal area generates a 1000 lb force. At joint 2 1000lb is applied on the joint horizontally with direction of 3 to 2. There is another 1000lb force from pipe 1-2 that is applied at j2, vertically up. Those forces are basically resisted by pipe tension, just as the momentum forces are. Tension in pipe 2-3 resists the horizontal pressure force at j2 and tension in pipe 1-2 resists the vertical force at j2. The tension in pipe 1-2 is balanced by a similar pressure force acting downward at joint 1. You can see that our balancing procedure is the same as what we did for the momentum forces.
To consider both pressure and momentum forces at the same time, just add all horiz force components together and all vertical forces together and balance one, then the other.
In the case of joint 3, or anywhere a joint has a force imbalance, we have to assume that bending moments will form up inside the pipe that will resist all forces that remains unbalanced by pipe axial force. Basically the unbalanced forces are resolved into shear forces acting perpendicular to pipe axes. The bending moment can be estimated by the shear force x pipe length.
You have to remember that we are trying to do this force distribution in a pipe structure that is usually very much indeterminate and we are making a lot of simplifying assumptions, so solutions are not exact and all forces and moments might not balance exactly. The goal is to reasonably reach a conservative, most probable, and plausible solution. It may take several iterations to develop a conclusion, redistributing any unbalanced forces and moments as you move from one iteration to the next. It helps if you know the basic principles of structural analysis, as pipe is a space frame, just made of "O-beams". Knowing how the structural analysis moment distribution method works is advantageous. I was a structural engineer before I started doing pipe stress.

![[thumbsup2] [thumbsup2] [thumbsup2]](/data/assets/smilies/thumbsup2.gif)