LAZAR90 - I assume you are asking about a "classical" solution
(without concern for how tedious that solution may be).
I'll outline one for you, superposition:
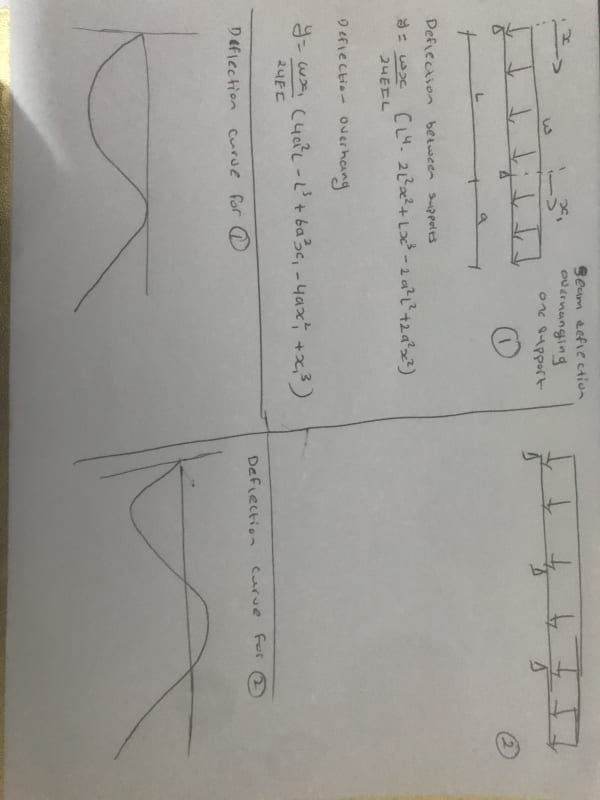
From any edition of the AISC Manual of Steel Construction refer to Beam Diagram #24:
Knowing the uniform distributed load, location of the three supports, location of the the end of the cantilever, and beam properties (E and I), ignore the middle support completely (as if it does not exist). Now solve for R
1, R
2, deflection at the location of the ignored middle support, and deflection at the point of interest.
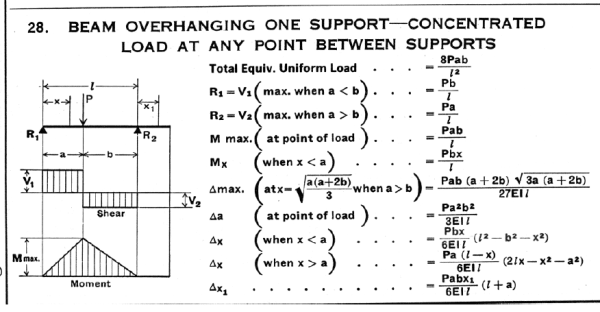
Now refer to Diagram #28:
Force "P" is placed at the middle support. Calculate the value of "P" need to make defection equal zero at that point. Pay attention of the sign (positive or negative) of "P". Same applies for calculated deflections.
With value of "P" now known, calculate deflection at the point of interest.
For the point of interest, algebraically sum the deflections from the two diagrams... this is your "answer". Now pull out your calculator (or slide rule) and get to work.
I know good-and-well that no one would really use this complex method today, but it does give a (mathematically) correct solution. A fringe benefit being that with the attention to detail needed for accuracy, you will get an opportunity to really understand what is happening a beam loaded this way... not just an "answer".