Basic frame problem [Solved] 3

[David_G_]

Hi all,

I'm trying to refresh my knowledge from my BSc mechanical engineering degree 4 years ago and this specific structural frame problem has me stuck. There must be some basic line of thinking I've forgot.

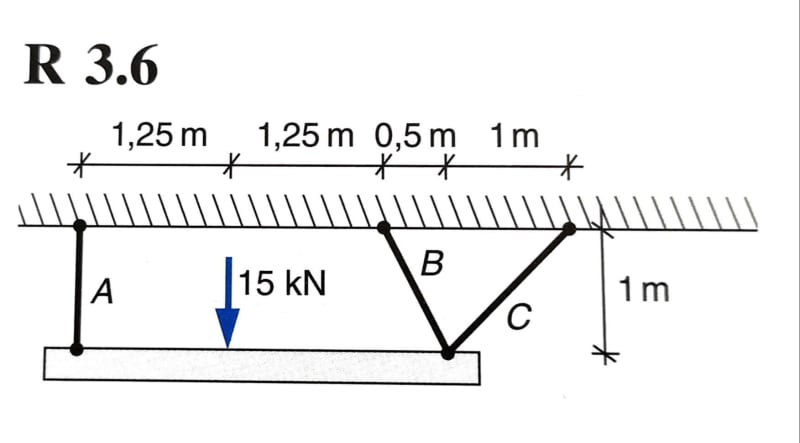
Task: Find forces in A, B and C.

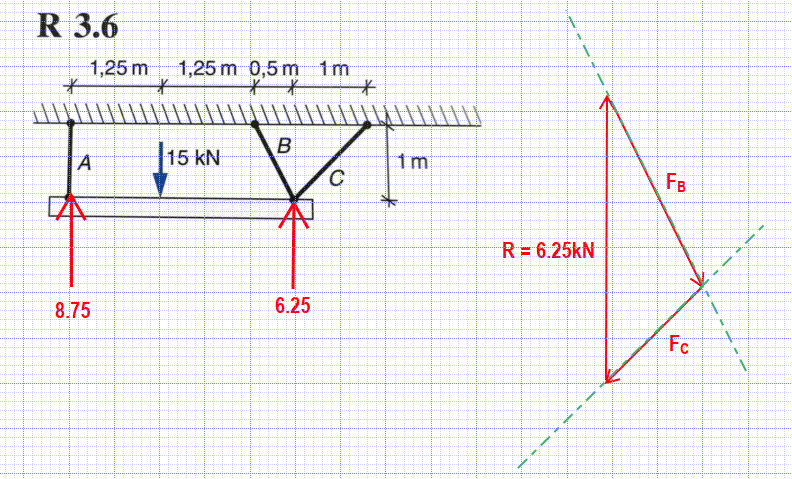
I start by making a free body diagram, and split B and C forces in their X and Y components.
I find force A by calculating the net moment on intersection between B and C: Force A = 8,75kN.

Net force in Y-direction gives F_by+F_cy= 6,25kN.
Net force in X-direction gives F_bx = F_cx

From here on I'm stuck...

(Final answers are: F_A=6,25kN 8,75kN, F_B=4,66kN, F_C=2,95kN)

Edit: F_A=6,25kN 8,75kN
Edit2: Solution found. The basic line of thinking I forgot to use was trigonometric substitution in the equilibrium equations..

 

[WARose]

Assuming those are pinned connections truss members.....I solved by first taking the moments about the point where the two truss members meet (to get F_A), then I summed forces in the F_y and F_x directions and solved simultaneous to get the answers. (Not the same as you got in the last line of your post.)

[red]EDIT[/red]: With your updated post, our answers match.

 

[ProgrammingPE]

You're on the right track. The force in A of 8,75kN is correct (although you did write 6.25kN as the final answer), and the two equations you have are also correct. You just need to come up with the additional equations by accounting for the angle of B and C. This will allow you to relate Fby to Fbx and Fcy to Fcx then you can solve the equations you have. You can then determine Fb and Fc since you'll know the vertical and horizontal components. Hope this helps!

Structural Central

http://www.structuralcentral.com

http://www.youtube.com/channel/UCOj2mXXf3ZbZtgxTc6BtkGg

 

[BAretired]

The beam is supported by a roller support at the left and a pin support at the right. The reactions are 8.75kN at the left and 6.25kN at the right.

F_A is 8.75kN by inspection. F_B and F_C are the forces which produce 6.25kN vertical, which can be found graphically (see below). The force in members B and C can be found using trigonometry, but if the reaction force is drawn to scale, they can also be scaled with sufficient precision for most purposes.

BA

 

[David_G_]

Hi all!

Lots of great advice here. Yes, the last line in my post was wrong, and is now corrected.

WARose: How do you combine them whem solving simultaneous? I've written what I found with net sum X and Y directions. Did you use trigonometry to combine the equations into one another?

ProgrammingPE: I'm trying this right now. I'll come back with what I find.

BAretired: Have you also found B and C forces individually? I agree the vertical is 6,25kN

 

[WARose]

WARose: How do you combine them whem solving simultaneous?

Just added them together. I first multiplied the Fx set of equations by -1. That enabled me to eliminate the F_c term and solve for F_B. The rest is pretty straight forward.

 

[BAretired]

BAretired: Have you also found B and C forces individually? I agree the vertical is 6,25kN

No, I haven't done that, but I drew the stress diagram to scale, so I would estimate Fb to be about 4.8kN and Fc to be about 3.1kN.

BA

 

[WARose]

No, I haven't done that, but I drew the stress diagram to scale, so I would estimate Fb to be about 4.8kN and Fc to be about 3.1kN.

I came out with the last line in the (updated) OP being correct. And as a sanity check, I did it on STADD and got the same thing (aside from a lot of warnings about out-of-plane stability and so on ).

 

[David_G_]

Hi all,

ProgrammingPE:
I've managed to solve this problem now. F_B=4,66kN and F_C=2,95kN by using the X and Y net force equations:
Net force in Y-direction gives Fby+Fcy= 6,25kN. (Eq. I)
Net force in X-direction gives Fbx = Fcx (Eq. II)
And using some basic trigonometry: Substitue both terms in Eq. I with their Fbx terms by trigonometry. (Fby=Fbx/tan(26,57)=Fbx/0,5 and Fcy=Fcx/tan45=Fcx/1=Fcx).
Solve to find Fbx, and then find the rest with vector sums and trigonometry.. Thank you!

WARose:
Even though I've solved the problem with trigonometry, I'd still be interesting in your way to solve it. I must admit there are some parts of your explanation I still don't fully get.
My understanding at the moment is that there are really only two X or Y equations:
Net force in Y-direction gives Fby+Fcy= 6,25kN. (Eq. I)
Net force in X-direction gives Fbx = Fcx (Eq. II)
I believe I would understand your method if I understood how you get more equations than these two for the object. I'm thinking mostly through the three equilibrium equations.


BAretired:
Interesting way to look at the problem. Your estimations are quite good enough to be usable. Thank you!

 

[BAretired]

When I scale dimensions, I tend to err on the safe side. Looking at the stress diagram from my previous post, it is clear that:
1. F_B*cosθ + F_C/√2 = 6.25 where θ = tan^-10.5 = 26.565^o
2. F_B*sinθ = F_C/√2

Solving these two simultaneous equations, I get 4.66 and 2.94 for Fb and Fc respectively.

BA

 

[WARose]

Even though I've solved the problem with trigonometry, I'd still be interesting in your way to solve it. I must admit there are some parts of your explanation I still don't fully get.

See attached for my calcs.

 

[BAretired]

My understanding at the moment is that there are really only two X or Y equations:
Net force in Y-direction gives Fby+Fcy= 6,25kN. (Eq. I)
Net force in X-direction gives Fbx = Fcx (Eq. II)
I believe I would understand your method if I understood how you get more equations than these two for the object. I'm thinking mostly through the three equilibrium equations.

The third equilibrium equation is the sum of moments = 0. That was used in determining beam reactions, but is not needed to determine bar forces which meet at a pin joint where the moment is known to be zero.



BA

 

[rb1957]

another day in paradise, or is paradise one day closer ?

 

[David_G_]

See attached for my calcs.

I see. So basically you use the ΣFY and ΣFX equations, but substitute the Y and X force components for B and C with their hypotenuse equations, and skip using trigonometry since we know all 3 sides of the triangle, and the forces through the objects act like pin-jointed trusses (forces only moving parallel through the objects).
Thank you, now I understand. I was starting to wonder if you solved this without exploiting geometry math