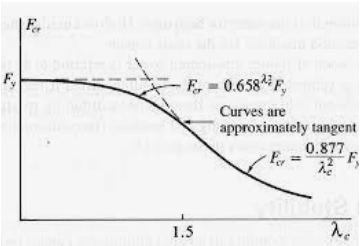
Equation E3-4: Fe = (pi^2)E / (L/r)^2
This represents the elastic buckling stress, right? Pure Euler buckling theory.
Substitute this into Equation 3-3 (Fcr = 0.877Fe) and you've got the code specified elastic buckling strength. It doesn't 100% follow buckling theory because of that 0.877 reduction. But, you understand that concept.
Equation E3-2, on the other hand, is supposed to represent the critical buckling strength when the column is controlled by INELASTIC buckling. In order to calculate this, we need to know the euler buckling stress and the yield strength.... Because this Fy/Fe ratio tells us where we fall on the inelastic buckling curve. Essentially, how much inelasticity are we going to see in the column when it buckles.
If you plot out these equations in excel for various L/r ratios, you will see that this doesn't actually decrease the capacity for L/r values that are lower than the the limiting value (4.71(sqrt (E/Fy)). Instead, it increases those values. But, it increases at a much slower rate than would be expected if this were based on L/r alone.