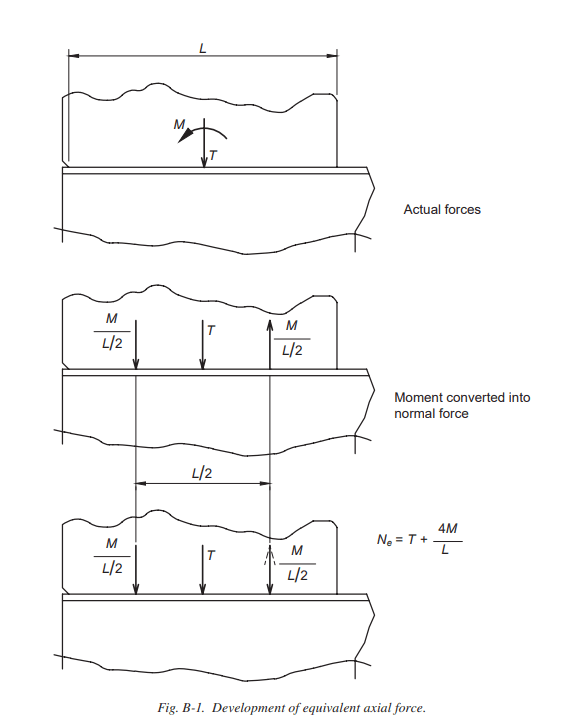
DG29 authors decouple the moment into a normal force, applied at 1/4 points along the gusset edge. Rearranging the moment equation (M=r*L/2), the resultant is r=2M/L.
DG 29 states "The authors base the calculations on the largest resultant normal stress, though obviously the moment will add to the axial stress on one side and subtract on the other" (DG29 pg 371).
The forces acting on the additive "left half" of the gusset edge are N_left_half= T/2 + 2M/L. The above quote, coupled with the reversed dashed arrow in Fig. B-1, leads me to believe the authors intend for designers to neglect the effect of the "right half" (where the normal force T/2 and moment resultant are in opposite directions N_right_half= T/2 - 2M/L).
So if we think about designing each half of the gusset for the additive "left half" forces, we get N_equiv = 2*N_left_half = 2*[(T/2)+(2M/L)]= T + 4M/L.
This is reinforced by the wording on AISC Seismic Design Guide 3rd Ed (blue book), page 5-209. "Over half the gusset, the normal force is N/2 + 2M/L, and over the other half it is N/2-2M/L. For simplicity of calculations, one of the moment forces, 2M/L, is reversed so that a uniform equivalent normal force exists over the entire gusset edge."
Sorry if that was too wordy.