Hi,
I'm implementing a simple CFD simulator following the book "Numerical Simulation in Fluid Dynamics - A Practical Introduction" by Griebel/Dornseifer/Neunhoeffer and I was obtaining the weird behaviour that temperature was changing in the fluid just because of velocity gradients (I mean, the domain is initially set to uniform temperature in every point, and then, just because of velocity gradients, it starts to change).
Trying to find out the reason, maybe it's related to the way they suggest to implement the energy equation in the book:
They start by stating the equation as:
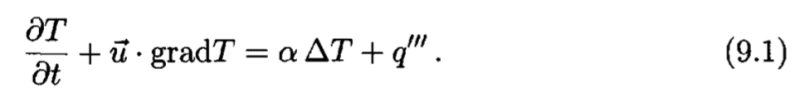
Then, when doing the particularization to two dimensions, they arrange the equation as:
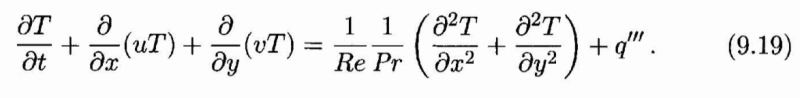
...and this puzzles me, because, I see they are understanding "u*grad T" as "grad(u*T)" instead of "u*(grad T)", or even "(u * grad)T".
For example, I would expect the product "u*grad T" in the lines of (taken from Wikipedia):
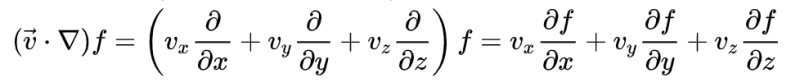
At the end, they show the discretization for the equation, in this form:
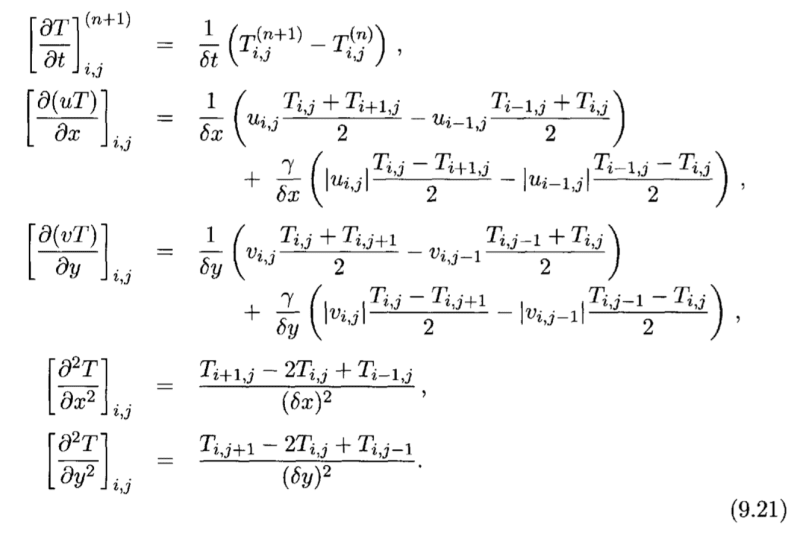
...and these equations clearly show the weird behaviour that I'm getting. Imagine for example the scenario I was mentioning at the beginning: constant temperature across the whole domain, with only variations in velocities. If you understand "u*grad T" as "u*(grad T)", then there's no change in temperature, because the gradient of T is zero (and this is the behaviour I would expect). However, if you understand "u*grad T" as "grad(u*T)", then even if the temperature is constant, any change in the velocity will lead to a change in temperature.
Is there something I'm not understanding correctly, or should I take "u*(grad T)" instead, as my common sense suggests?
Thanks!
I'm implementing a simple CFD simulator following the book "Numerical Simulation in Fluid Dynamics - A Practical Introduction" by Griebel/Dornseifer/Neunhoeffer and I was obtaining the weird behaviour that temperature was changing in the fluid just because of velocity gradients (I mean, the domain is initially set to uniform temperature in every point, and then, just because of velocity gradients, it starts to change).
Trying to find out the reason, maybe it's related to the way they suggest to implement the energy equation in the book:
They start by stating the equation as:
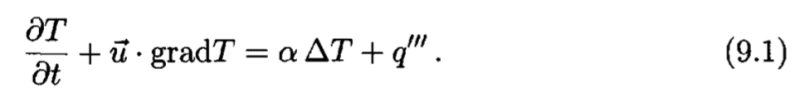
Then, when doing the particularization to two dimensions, they arrange the equation as:
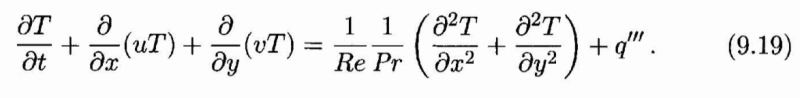
...and this puzzles me, because, I see they are understanding "u*grad T" as "grad(u*T)" instead of "u*(grad T)", or even "(u * grad)T".
For example, I would expect the product "u*grad T" in the lines of (taken from Wikipedia):
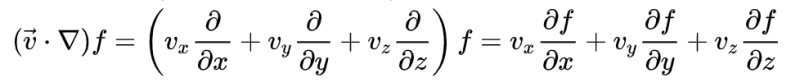
At the end, they show the discretization for the equation, in this form:
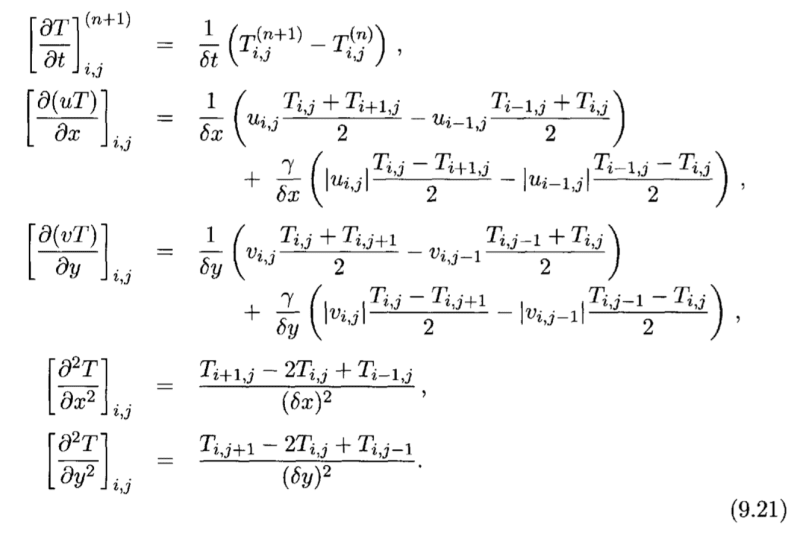
...and these equations clearly show the weird behaviour that I'm getting. Imagine for example the scenario I was mentioning at the beginning: constant temperature across the whole domain, with only variations in velocities. If you understand "u*grad T" as "u*(grad T)", then there's no change in temperature, because the gradient of T is zero (and this is the behaviour I would expect). However, if you understand "u*grad T" as "grad(u*T)", then even if the temperature is constant, any change in the velocity will lead to a change in temperature.
Is there something I'm not understanding correctly, or should I take "u*(grad T)" instead, as my common sense suggests?
Thanks!
