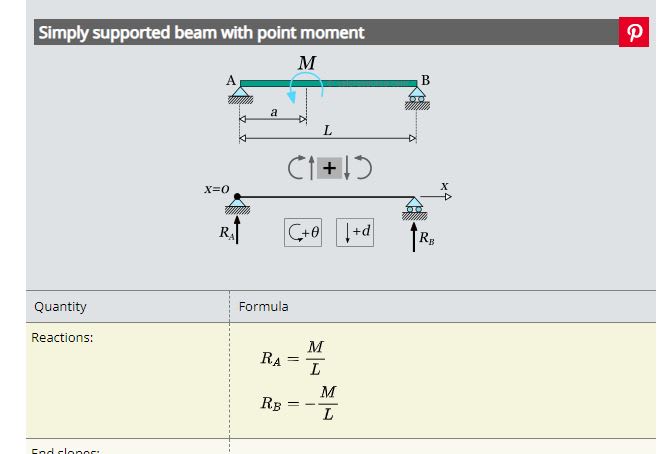
Hi All,
I'm having some issues with probably a basic force and moment resolving equation. I basically have a conveyor pulley that is mounted on a trolley with with 4 wheels on a rail. The pulley has two opposing and equal forces (f1 and f2). f1 represents the tension of the belt against the pulley and f2 on the otherside is a sheave attached to a winch via rope. F1 acts eccentrically to the centre of the pulley (the belt is not tracking centrally) at a distance of d1 thereby creating a turning moment. this turning moment wants to rotate the trolley and thus created an axial reaction force acting on the four wheels. note that the rail and wheel contact is preventing the trolley from turning
i am trying to resolve the force acting on the wheels (R1 and R2) but i am not sure of my free body diagram is correct or not and if i have resolved these forces correctly.
any help is appreciated.
image of the problem below
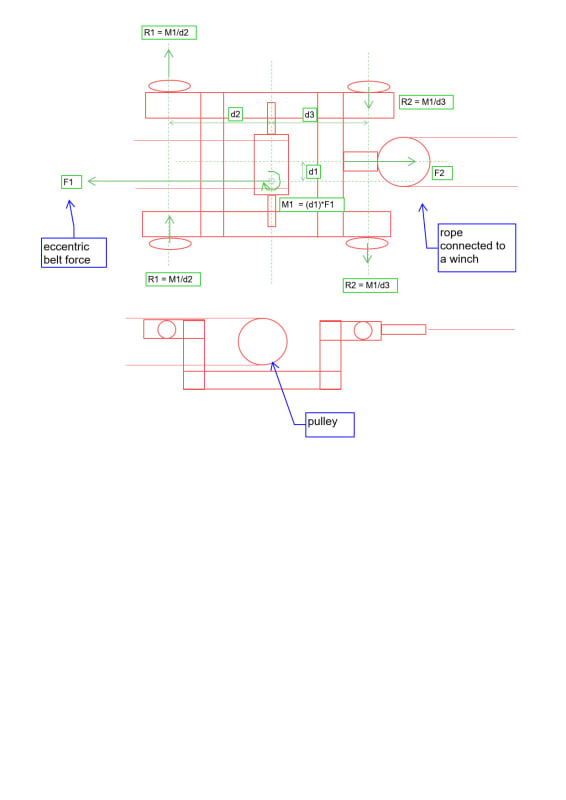
I'm having some issues with probably a basic force and moment resolving equation. I basically have a conveyor pulley that is mounted on a trolley with with 4 wheels on a rail. The pulley has two opposing and equal forces (f1 and f2). f1 represents the tension of the belt against the pulley and f2 on the otherside is a sheave attached to a winch via rope. F1 acts eccentrically to the centre of the pulley (the belt is not tracking centrally) at a distance of d1 thereby creating a turning moment. this turning moment wants to rotate the trolley and thus created an axial reaction force acting on the four wheels. note that the rail and wheel contact is preventing the trolley from turning
i am trying to resolve the force acting on the wheels (R1 and R2) but i am not sure of my free body diagram is correct or not and if i have resolved these forces correctly.
any help is appreciated.
image of the problem below