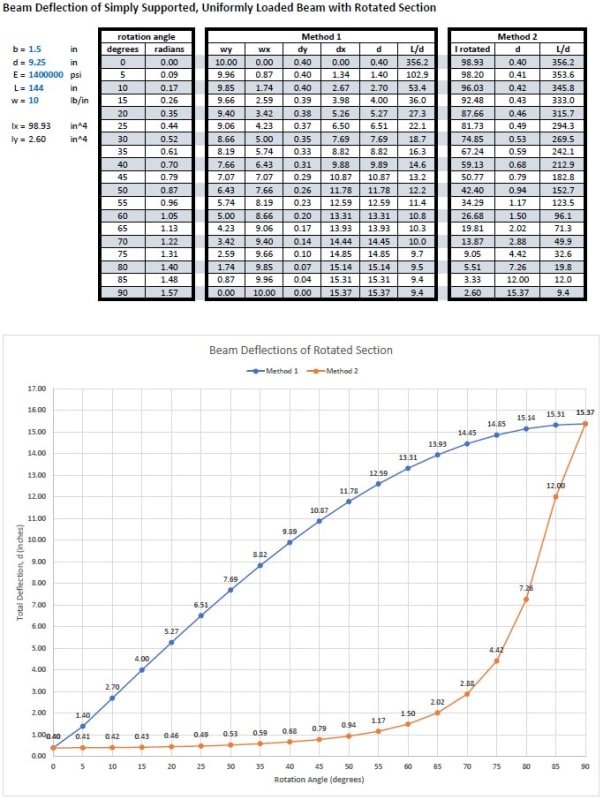
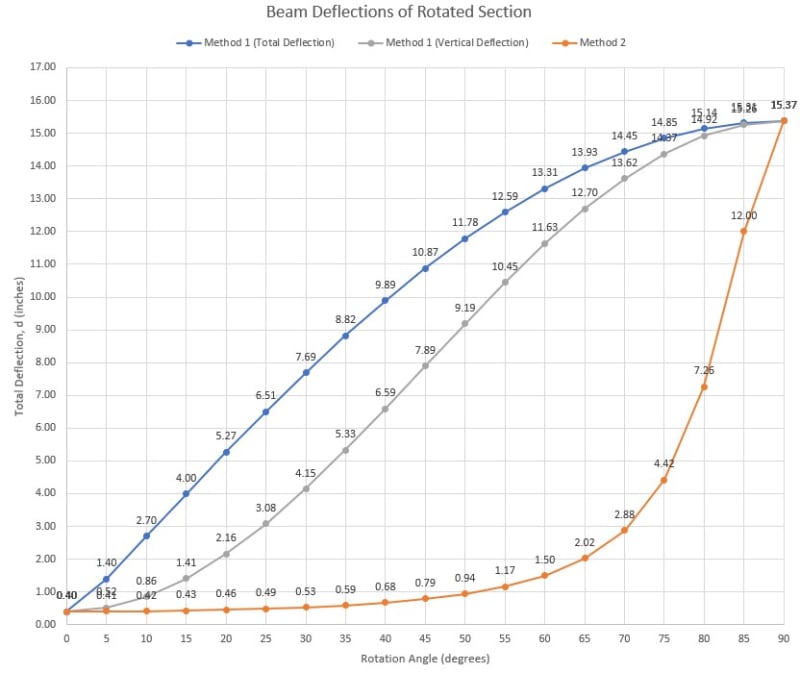
I'm working on a "simple" wood beam design tool. The beam can be rotated about it's longitudinal axis, with a rotation of 0 meaning that it's oriented in the strong direction for gravity loading, 90 degrees is a flatwise orientation, etc. The loads are always acting vertically (in the gravity direction) and for the sake of this discussion are assumed to act at the centroid/neutral axis (no torsion). The sketch below should clarify the basic conditions. I'm trying to calculate the total deflection of the beam under a uniform load for any rotation of the section. Despite scouring my resources and the internet, I can't find much guidance on this.
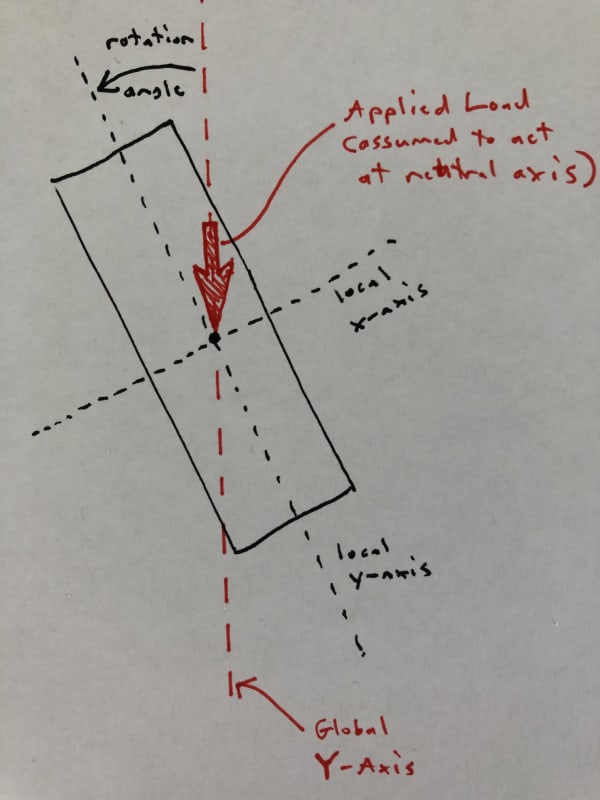
With the beam oriented either vertically or flat, the calculation is simple. I use either Ix (strong axis MOI) or Iy (weak axis MOI) of the section and the equation d = 5wL^4/384EI. For the rotated section, though, I can think of 2 different ways to calculate the total deflection, which give very different results:
Method 1:
[ol A]
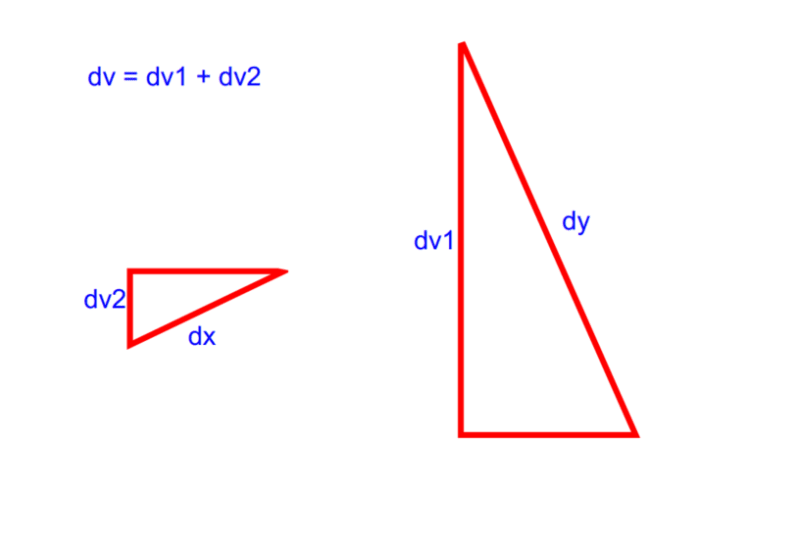
[li]Calculate the component of the load acting in the direction of the member's local y-axis. Then using this load (we'll call wy) and Ix, calculate the deflection, dy, which is the deflection in the direction of the member's local y-axis (strong axis).[/li]
[li]Using a similar procedure, calculate the deflection dx, in the direction of the member's local x-axis (weak axis).[/li]
[li]Calculate the total deflection: d = sqrt(dy*dy + dx*dx)[/li]
[/ol]
And Method 2:
[ol A]
[li]Given Ix and Iy, calculate I_rotated, which is the MOI with respect to the Global X-Axis, which is a horizontal line going through the centroid of the section (I should have included that in the sketch above). From my strength of materials text: I_rotated = (Ix+Iy)/2 + cos(2*angle)(Ix-Iy)/2[/li]
[li]With I_rotated calculated, calculate d from the equation above (using I_rotated in place of I).[/li]
[/ol]
I'll follow-up with a spreadsheet showing the large difference in values between the 2 methods.

With the beam oriented either vertically or flat, the calculation is simple. I use either Ix (strong axis MOI) or Iy (weak axis MOI) of the section and the equation d = 5wL^4/384EI. For the rotated section, though, I can think of 2 different ways to calculate the total deflection, which give very different results:
Method 1:
[ol A]
[li]Calculate the component of the load acting in the direction of the member's local y-axis. Then using this load (we'll call wy) and Ix, calculate the deflection, dy, which is the deflection in the direction of the member's local y-axis (strong axis).[/li]
[li]Using a similar procedure, calculate the deflection dx, in the direction of the member's local x-axis (weak axis).[/li]
[li]Calculate the total deflection: d = sqrt(dy*dy + dx*dx)[/li]
[/ol]
And Method 2:
[ol A]
[li]Given Ix and Iy, calculate I_rotated, which is the MOI with respect to the Global X-Axis, which is a horizontal line going through the centroid of the section (I should have included that in the sketch above). From my strength of materials text: I_rotated = (Ix+Iy)/2 + cos(2*angle)(Ix-Iy)/2[/li]
[li]With I_rotated calculated, calculate d from the equation above (using I_rotated in place of I).[/li]
[/ol]
I'll follow-up with a spreadsheet showing the large difference in values between the 2 methods.