I don´t get how to determine the vector r(AB). I know that i have to transmit the given angels. Please help me guys.
The Solution is r(AB) = (-√3*a,a,0)
Task:
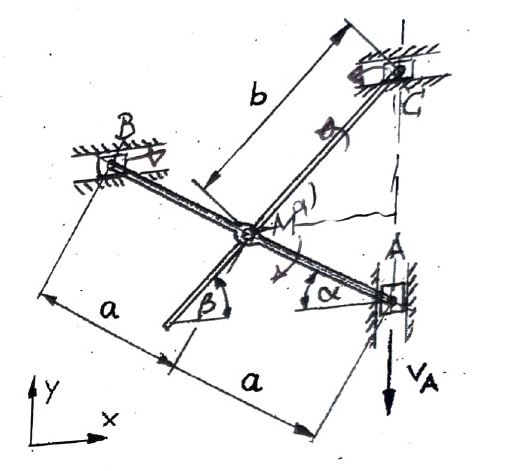
A rod 1 becomes vertical at its end A and at its
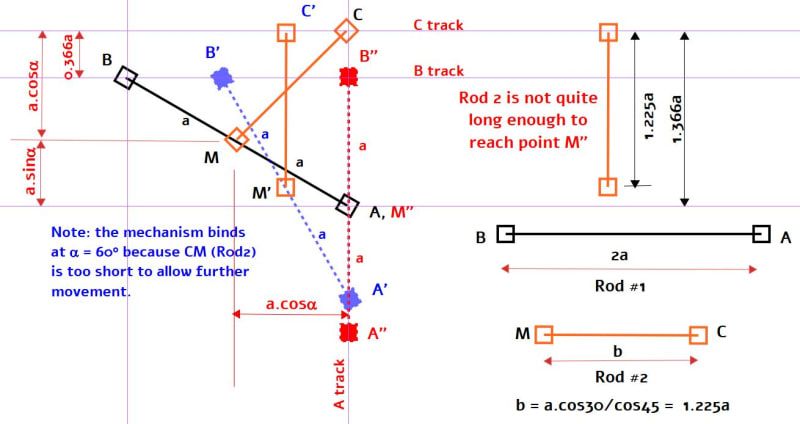
End B guided horizontally. In the middle M is a second one
Rod 2 is rotatably mounted, the end C of which is also horizontal
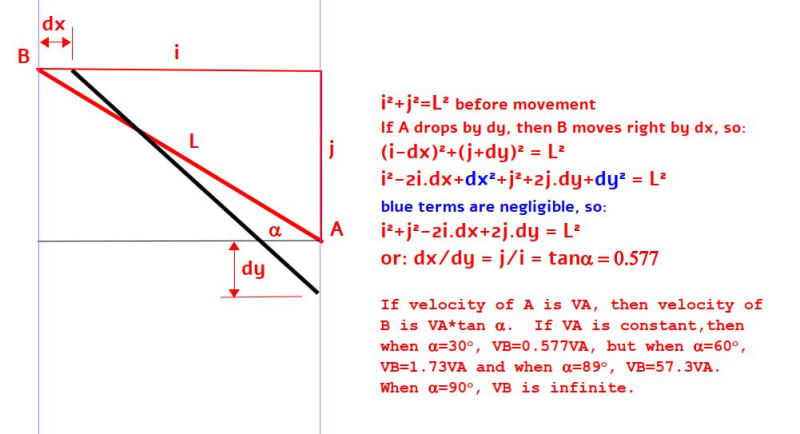
to be led. Point A moves at the constant speed
especially downwards.
a) Determine the velocities of points B and
C
Given: a, b, α =30°, β =45°, VA=const.
The Solution is r(AB) = (-√3*a,a,0)
Task:
A rod 1 becomes vertical at its end A and at its
End B guided horizontally. In the middle M is a second one
Rod 2 is rotatably mounted, the end C of which is also horizontal
to be led. Point A moves at the constant speed
especially downwards.
a) Determine the velocities of points B and
C
Given: a, b, α =30°, β =45°, VA=const.