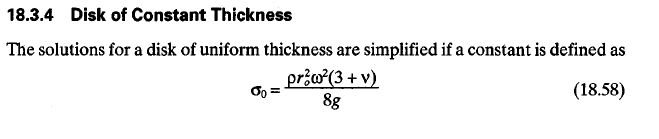Hi All,
Could you please check my calculations to see if I have this correct, it's been a while & need to check.
Stress in Flywheel
4140 Steel
Tensile strength 655 MPa 95000 psi
Yield strength 415 MPa 60200 psi
σt-max = d/4 * w^2 * ( 3+ v * R2^2 + (1-v) * R1^2
σt-max is the maximum internal stress in the flywheel N/m^2
d is the density of the flywheel material Kg/m^3
ω is the angular velocity of the flywheel rad/sec
v is the Poisson ratio of the flywheel material-Steel
The Factor of safety FOS can be calculated as
FOS = σ-yield / σt-max
Where
(σ yield) is the possible angular velocity when the maximum internal stress equals the yield stress of the material.
Flwheel Diam R2 = 0.15 radius mtrs
Flywheel inner dia R1 = 0.025 radius mtrs
Density of steel = 7850 Kg/m^3
Tensile strength = 655 Mpa
Pa = 655000000 Pascals
Poisson's ratio (v) = 0.3
ω max = 1571 rad/sec
Velocity = 235.65 m/s
rpm max = 15000
σt-max = d/4 * w^2 * ( 3+ v * R2^2 + (1-v) * R1^2
d/4 = 1962.5
ω^2 = 2468041
3+v = 3.3
R2^2 = 0.0225
1-v = 0.7
R1^2 = 0.000625
σt-max = 2343814.663 N/m^2
= 2.343814663 Mpa
FOS = σ yield / σt-max
= 415 Mpa / 2.343814663 Mpa
FOS = 177.0618 ??
The FOS appears to be very high do I have this correct?
Could you please check my calculations to see if I have this correct, it's been a while & need to check.
Stress in Flywheel
4140 Steel
Tensile strength 655 MPa 95000 psi
Yield strength 415 MPa 60200 psi
σt-max = d/4 * w^2 * ( 3+ v * R2^2 + (1-v) * R1^2
σt-max is the maximum internal stress in the flywheel N/m^2
d is the density of the flywheel material Kg/m^3
ω is the angular velocity of the flywheel rad/sec
v is the Poisson ratio of the flywheel material-Steel
The Factor of safety FOS can be calculated as
FOS = σ-yield / σt-max
Where
(σ yield) is the possible angular velocity when the maximum internal stress equals the yield stress of the material.
Flwheel Diam R2 = 0.15 radius mtrs
Flywheel inner dia R1 = 0.025 radius mtrs
Density of steel = 7850 Kg/m^3
Tensile strength = 655 Mpa
Pa = 655000000 Pascals
Poisson's ratio (v) = 0.3
ω max = 1571 rad/sec
Velocity = 235.65 m/s
rpm max = 15000
σt-max = d/4 * w^2 * ( 3+ v * R2^2 + (1-v) * R1^2
d/4 = 1962.5
ω^2 = 2468041
3+v = 3.3
R2^2 = 0.0225
1-v = 0.7
R1^2 = 0.000625
σt-max = 2343814.663 N/m^2
= 2.343814663 Mpa
FOS = σ yield / σt-max
= 415 Mpa / 2.343814663 Mpa
FOS = 177.0618 ??
The FOS appears to be very high do I have this correct?