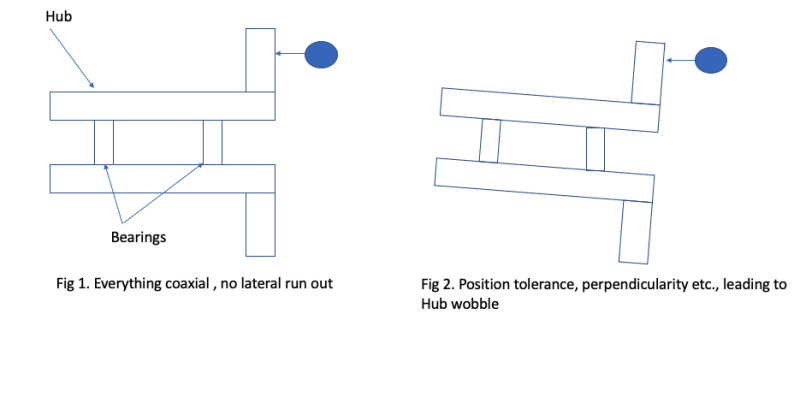
I am looking for an example of how to perform a tolerance stack up to check the worst case circular lateral run out.
I am only finding basic 1D stack examples , or 2D gap analysis type problems. Hoping someone could point me to a few good resources.
I have paged through Bryan R. FISCHER Mechanical Tolerance Stack book, but I do not see anything remotely similar to what I am trying to do.
I am only finding basic 1D stack examples , or 2D gap analysis type problems. Hoping someone could point me to a few good resources.
I have paged through Bryan R. FISCHER Mechanical Tolerance Stack book, but I do not see anything remotely similar to what I am trying to do.