Tygra_1983
Student
Hi there,
I am trying to solve a rigid frame that is supported by two pin supports. I am doing this using the unit load (or virtual work) method. To do this I am trying to create moment functions for each segement of the frame.
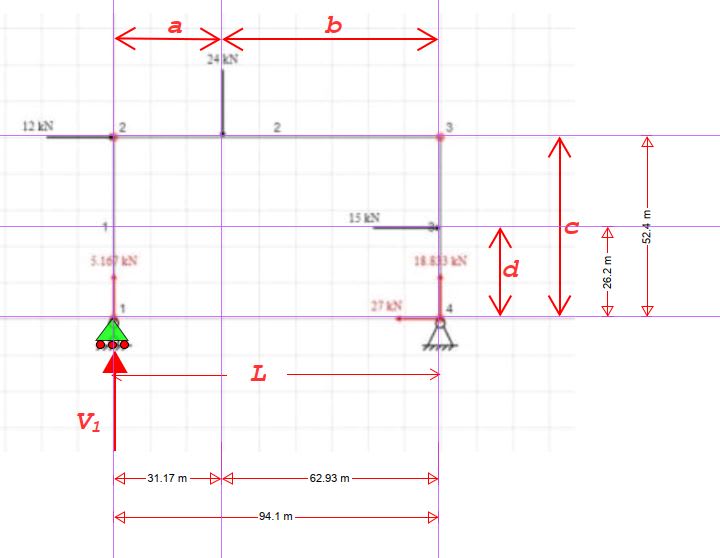
This is what my frame looks like:
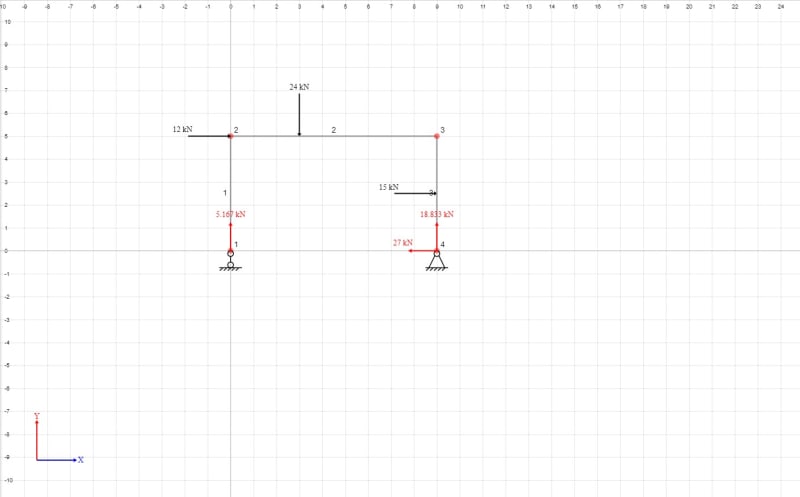
I have replaced the pin support at node 1 to a roller (which is what my text book said to do).
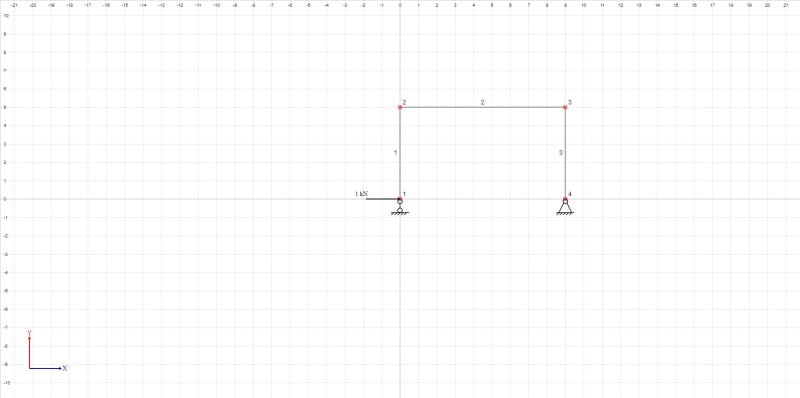
The virtual structure looks like the following:
For segment 2:3 I am attempting to create a moment function. I can do this easily with a beam in one dimension. However, because this is a frame I need to take the momenmt function in two directions.
The formula for virtual work across sgement 2:3 is:
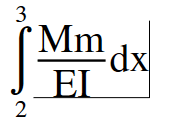
Where 'M' is the moment fuction of the real structure and 'm' is the moment function for the virtual structure.
Thus, I have created the moment function to be:
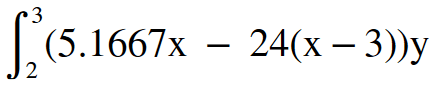
From here, I have tried solving this using the double inegral procedure, but I am not getting the correct result. Am I on the right path here, or am I wqay off?
I am trying to solve a rigid frame that is supported by two pin supports. I am doing this using the unit load (or virtual work) method. To do this I am trying to create moment functions for each segement of the frame.
This is what my frame looks like:

I have replaced the pin support at node 1 to a roller (which is what my text book said to do).
The virtual structure looks like the following:

For segment 2:3 I am attempting to create a moment function. I can do this easily with a beam in one dimension. However, because this is a frame I need to take the momenmt function in two directions.
The formula for virtual work across sgement 2:3 is:
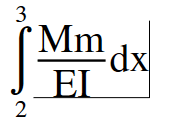
Where 'M' is the moment fuction of the real structure and 'm' is the moment function for the virtual structure.
Thus, I have created the moment function to be:
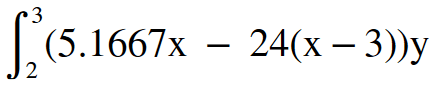
From here, I have tried solving this using the double inegral procedure, but I am not getting the correct result. Am I on the right path here, or am I wqay off?