TrustButVerify
Mechanical
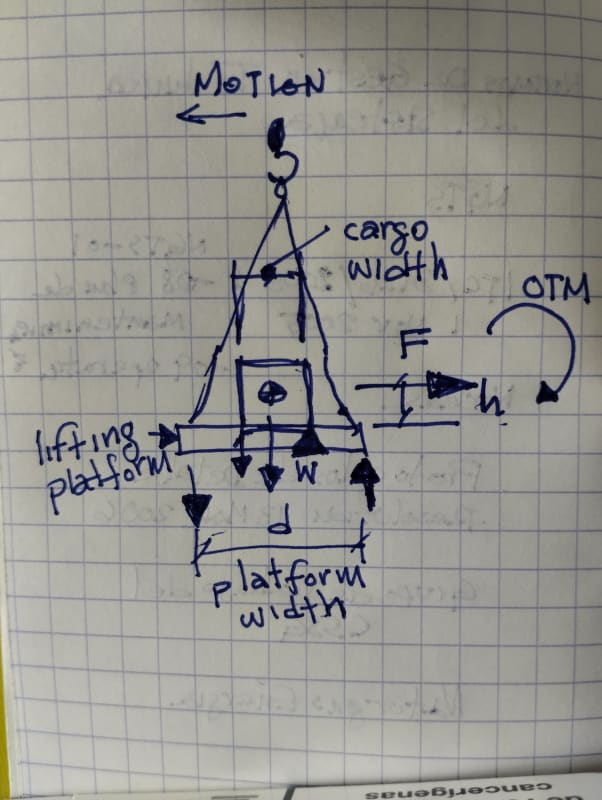
I'm scratching my head nowadays trying to understand how to approach the lifting of a cargo load by a gantry hydraulic crane.
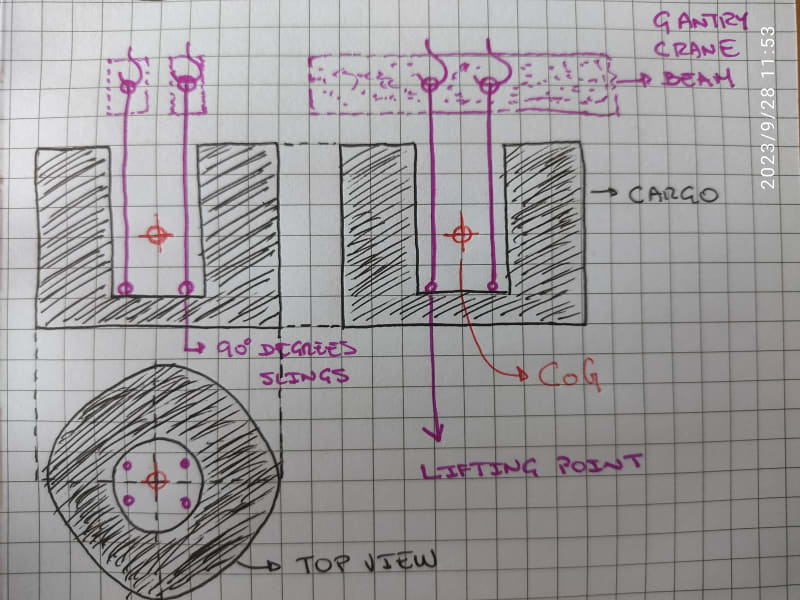
Cargo has 4 lifting points, and they are quite close to each other (relative to cargo length and width) around the geometric center of the cargo.
Four lifting points are quite below the CoG.
I'm concerned external forces might be a risky factor when the gantry starts to move over rails to move this cargo from A to B.
Cargo has 4 lifting points, and they are quite close to each other (relative to cargo length and width) around the geometric center of the cargo.
Four lifting points are quite below the CoG.
I'm concerned external forces might be a risky factor when the gantry starts to move over rails to move this cargo from A to B.