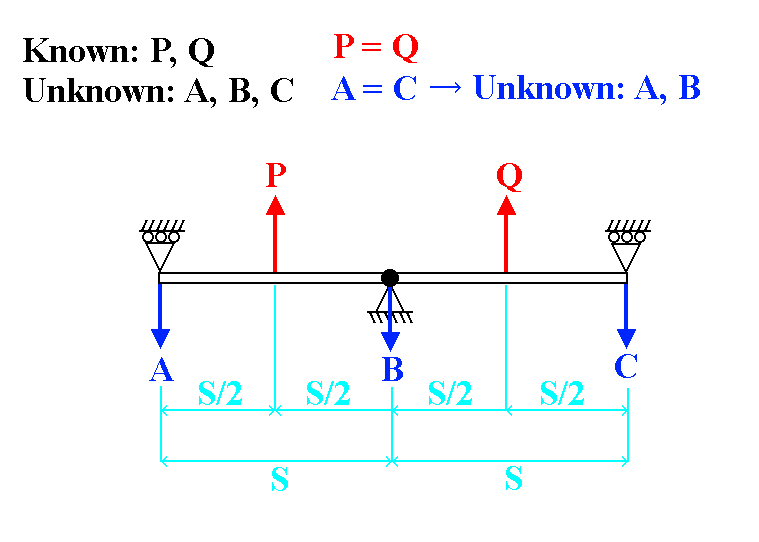
(See image)
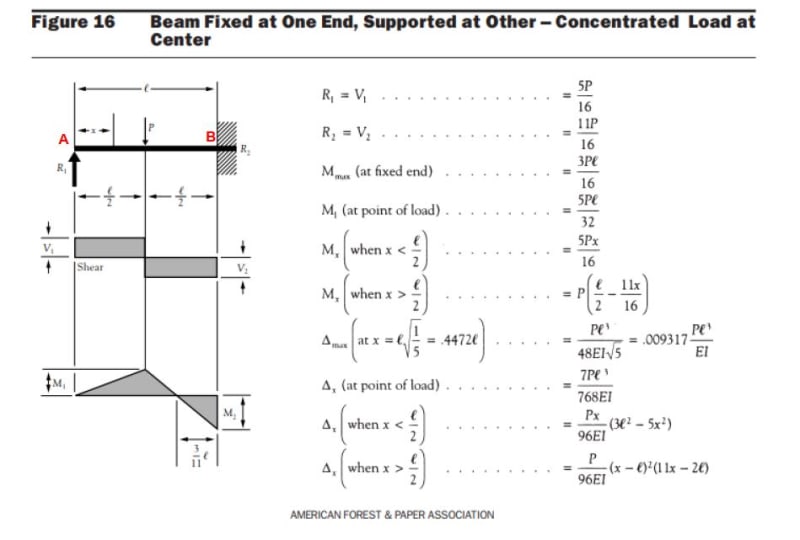
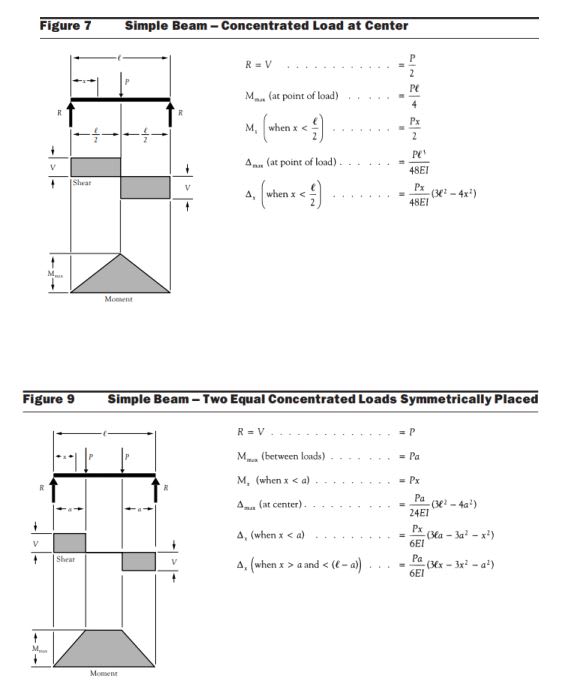
P = Q (They are the applied loads)
Unknowns are the reactions A, B, and C.
A and C are known to be equal however, so there are really only 2 unknowns.
A, B, and C are known to all be pointing downward.
At first glance this looks like a pretty easy/standard statics problem. But this has actually been giving me a lot of trouble, and I suspect it might be because I'm forgetting some sort of basic principle that I've perhaps been taking for granted up til now, which maybe happens to uniquely cause issues with this problem.
I've actually been a practicing engineer for a few years now. I make free-body diagrams all the time and solve statics problems on a regular basis. I feel that my statics foundation is pretty solid. But this problem has kind of humbled me--maybe it's just a brain fart, or maybe I've constructed a problem that isn't actually possible to solve for reasons not currently apparent to me.
Every time I try to solve this problem, attempting to solve the moment-sum equation combined with the force-sum equation eventually results in a trivial 0 = 0 identity, which means (by my understanding) that the equations were not truly independent. Normally, these equations absolutely should be independent however, so I suspect there is some other kind of issue going on here--OR maybe they really are not independent, in which case I would like to know what makes them non-independent, and how I can make sure to avoid constructing such problems in the future.
Or maybe it's statically indeterminate, despite there only being 2 unknowns?
(There was also a time I tried to solve a less-simplified version of this problem, and the solution told me that B was actually pointing upward. I definitely insist it should be pointing downward with the others, though)
Or maybe one of you guys will just solve this in five minutes and I'll realize I've just missed something obvious.
Curious to hear your thoughts/commentary.

![[wink] [wink] [wink]](/data/assets/smilies/wink.gif) ). With P midway of A and B the solution gives B/2=2.2 A, where B is the reaction in the original beam, and B/2 is of course the reaction in the cut beam So your result is correct!
). With P midway of A and B the solution gives B/2=2.2 A, where B is the reaction in the original beam, and B/2 is of course the reaction in the cut beam So your result is correct! ![[medal] [medal] [medal]](/data/assets/smilies/medal.gif)