Several examples from a publication on how to convert a three-phase concentric winding to a double-layer lap winding are found online.
The displayed table shows the value of the conversion factor in the case of a 54-slot, 2-pole, mixed winding ( 30 coils in total) with pitches of 1-20, 22, 24, 26, 28, and turns ratios of N, N, N, N, 0.5N, respectively.
On the right side of the table, conversion factors to lap winding are shown for various winding pitches from 1-15 to 1-28.
The number of turns per phase of the new winding is obtained by multiplying the number of turns per phase of the original winding by a correction factor. PROBABLY. I am not sure.
However, I've attempted to calculate these correction factors, but I couldn't obtain the values shown.
At first glance, it seems to me that the values of all the correction factors in this example must be greater than or equal to 1. Or I am missing something?
Is there anyone who can explain this and confirm if the displayed table is correct?
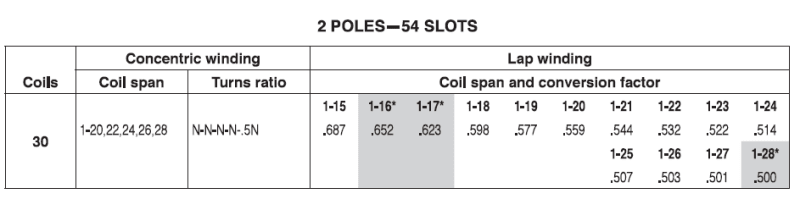
The displayed table shows the value of the conversion factor in the case of a 54-slot, 2-pole, mixed winding ( 30 coils in total) with pitches of 1-20, 22, 24, 26, 28, and turns ratios of N, N, N, N, 0.5N, respectively.
On the right side of the table, conversion factors to lap winding are shown for various winding pitches from 1-15 to 1-28.
The number of turns per phase of the new winding is obtained by multiplying the number of turns per phase of the original winding by a correction factor. PROBABLY. I am not sure.
However, I've attempted to calculate these correction factors, but I couldn't obtain the values shown.
At first glance, it seems to me that the values of all the correction factors in this example must be greater than or equal to 1. Or I am missing something?
Is there anyone who can explain this and confirm if the displayed table is correct?

