PatrickdG1998
Student
Hi all,
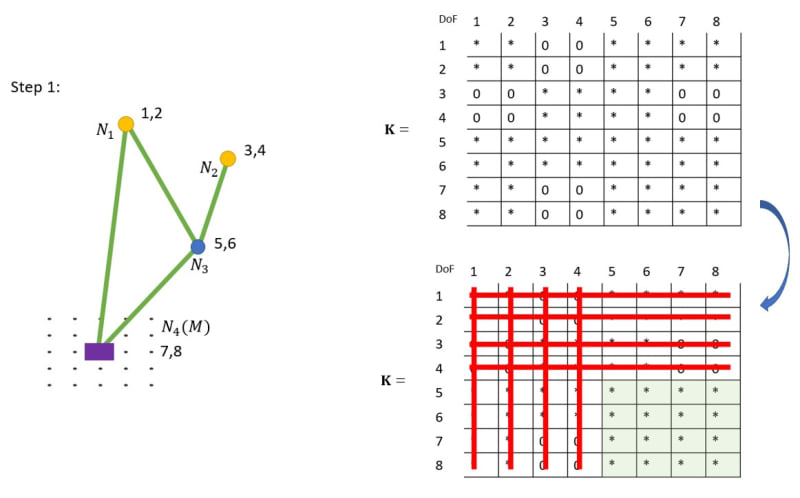
Right now I'm working on a mechanical mechanism where nodes are connected via "spring beams". This is very comparable of doing planar truss analysis, but now the deformations are large compared to the system.
In my analysis, one of the nodes undergoes a predefined deformation, and the rest of the free nodes are moving accordingly, which is calculated via the well known {f} = [K]{d}, where K is the global system stiffness matrix, and d is the displacement vector. Hereby: [K] = [T]^T [K_loc] [T]
When all displacements are known, {f} = [K]{d} is used again to calculate all corresponding forces. I'm interested in the force needed (in x,y-direction) of the node which got the predefined deformation. Because the deformations are relatively high, this process is done incrementally.
Now, I want to include a pre-tension in the mechanism. As trivial as it sounds, I didn't find much information about that in various papers.
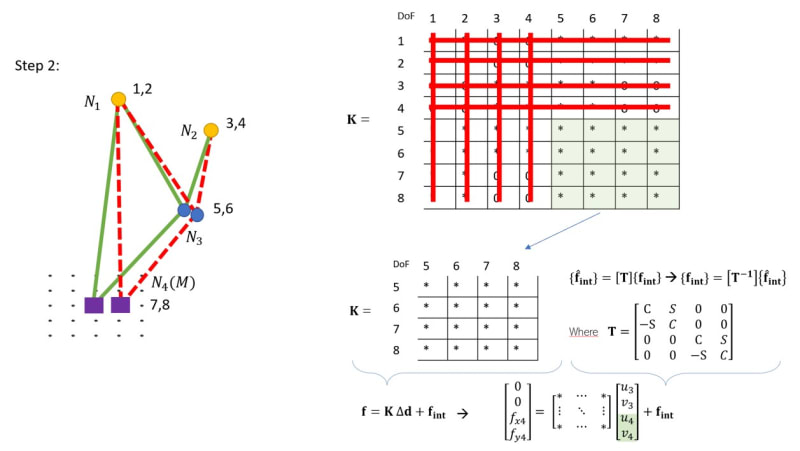
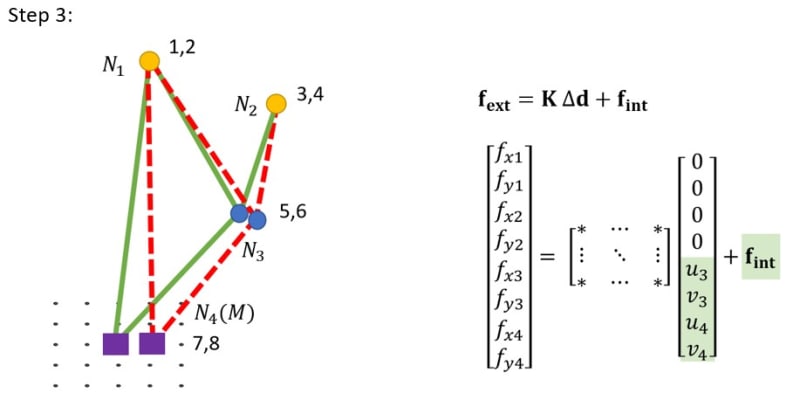
From intuition, I would suggest that the total force in the nodes is just a summation of f = [K]{d} and the global pretension vector: {f_ext} = [K]{d} + {f_int}, where f_int is the global pretension vector {f_int} = [T]^T {f_loc}. However, the global stiffness matrix should be modified by the pretension, since the pretension makes the whole mechanism stiffer. But using the aforementioned reasoning, this is not happening.
Therefore, I'm wondering if I make any mistake in this reasoning. Any help would be greatly appreciated.
In addition to that, any tips about papers/books involving pre-tensioning using the direct stiffness method would be very helpful.
Thank you in advance!
Right now I'm working on a mechanical mechanism where nodes are connected via "spring beams". This is very comparable of doing planar truss analysis, but now the deformations are large compared to the system.
In my analysis, one of the nodes undergoes a predefined deformation, and the rest of the free nodes are moving accordingly, which is calculated via the well known {f} = [K]{d}, where K is the global system stiffness matrix, and d is the displacement vector. Hereby: [K] = [T]^T [K_loc] [T]
When all displacements are known, {f} = [K]{d} is used again to calculate all corresponding forces. I'm interested in the force needed (in x,y-direction) of the node which got the predefined deformation. Because the deformations are relatively high, this process is done incrementally.
Now, I want to include a pre-tension in the mechanism. As trivial as it sounds, I didn't find much information about that in various papers.
From intuition, I would suggest that the total force in the nodes is just a summation of f = [K]{d} and the global pretension vector: {f_ext} = [K]{d} + {f_int}, where f_int is the global pretension vector {f_int} = [T]^T {f_loc}. However, the global stiffness matrix should be modified by the pretension, since the pretension makes the whole mechanism stiffer. But using the aforementioned reasoning, this is not happening.
Therefore, I'm wondering if I make any mistake in this reasoning. Any help would be greatly appreciated.
In addition to that, any tips about papers/books involving pre-tensioning using the direct stiffness method would be very helpful.
Thank you in advance!