Saleh abbasi
Mechanical
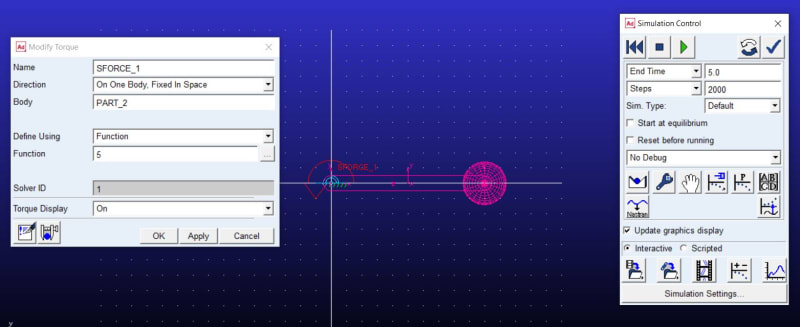
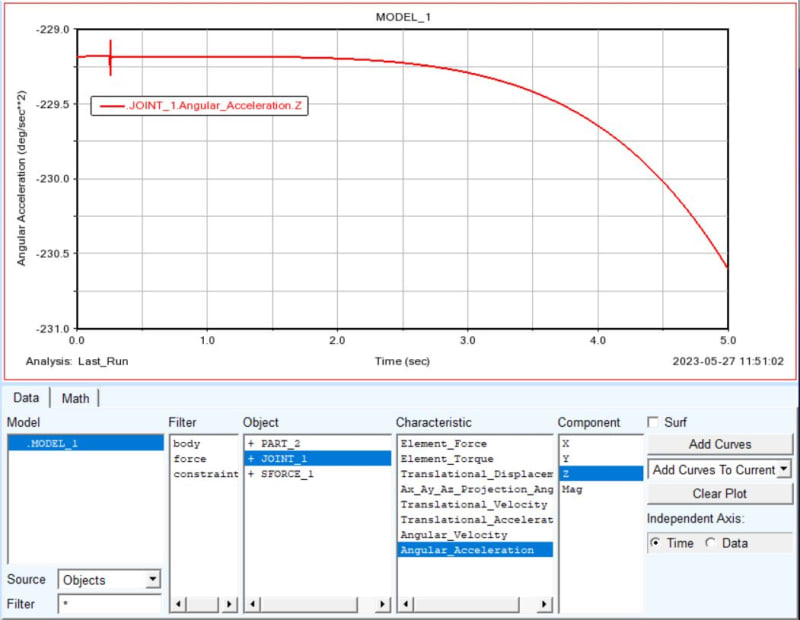
Hello everyone, I apologize for using this platform to ask my question. In Adams software, I am currently working on a simulation where I am applying a constant torque to a link that behaves like a pendulum. The system has no other forces acting on it, such as gravity or friction. According to the formula T=I*alpha, the relative angular acceleration should remain constant throughout the simulation. However, I have observed that in some instances, the acceleration becomes zero while in others it continues to increase.
I am seeking advice on how to obtain accurate and consistent results in my simulation. Any suggestions or recommendations would be greatly appreciated.
I am seeking advice on how to obtain accurate and consistent results in my simulation. Any suggestions or recommendations would be greatly appreciated.