StathPol12
Aerospace
Hi guys,
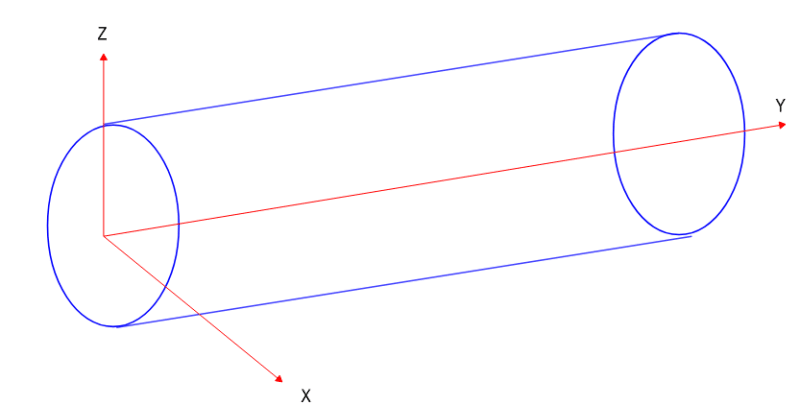
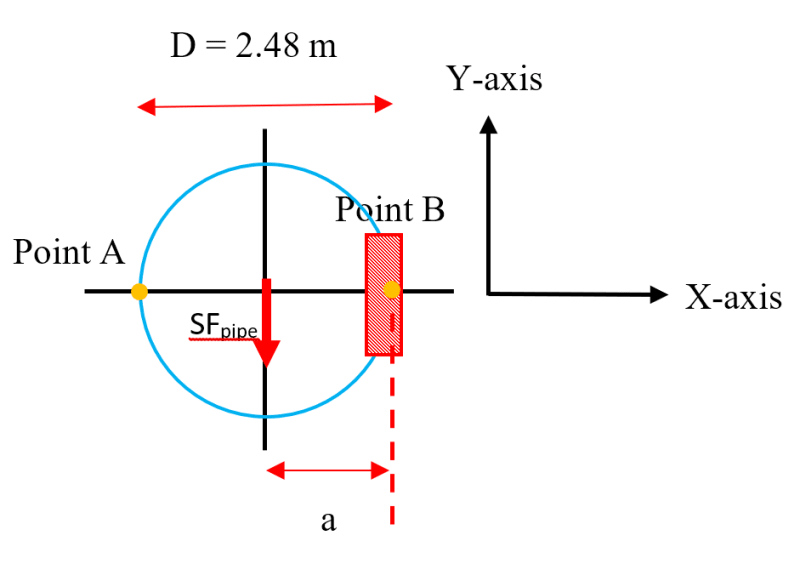
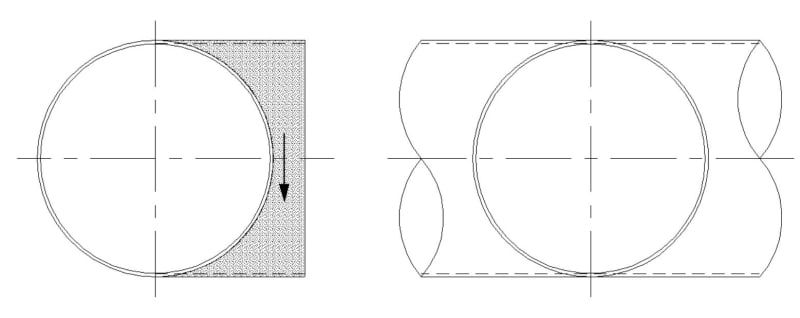
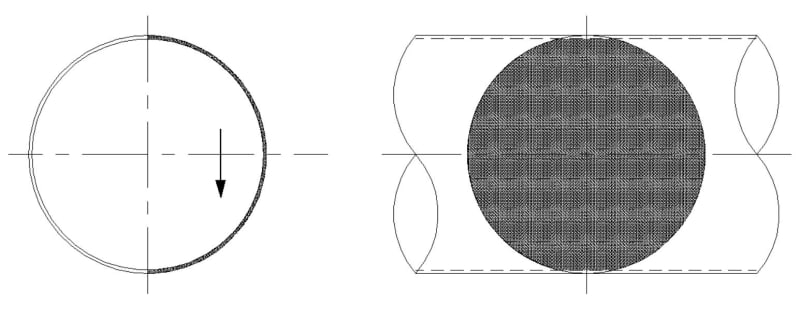
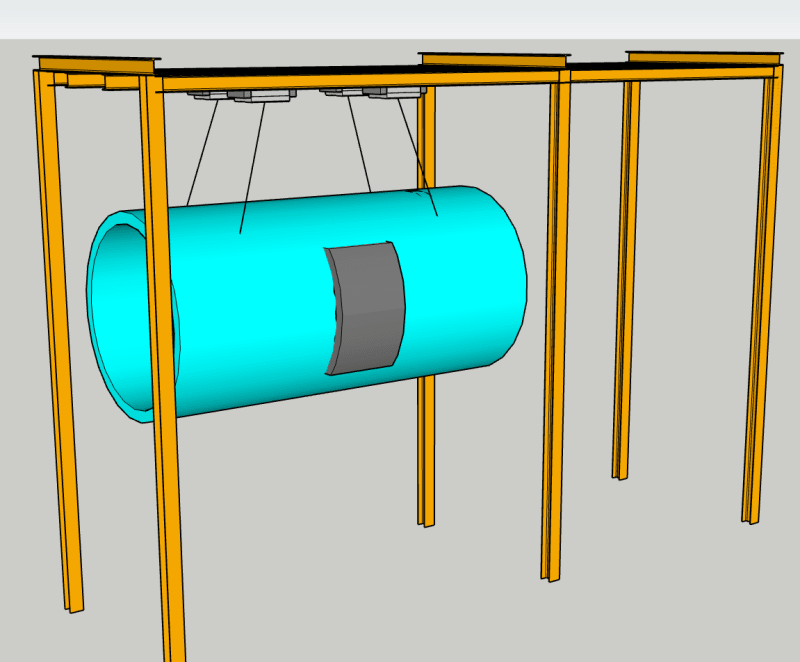
I have a steel pipe with the dimensions shown below:
Length of the pipe = 6.4 metres.
External diameter = 2.48 metres.
Internal diameter = 2.46 metres.
Self-weight of the steel pipe = 6766.85 kg (uniform steel pipe).
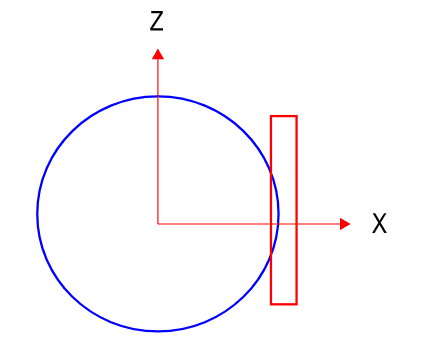
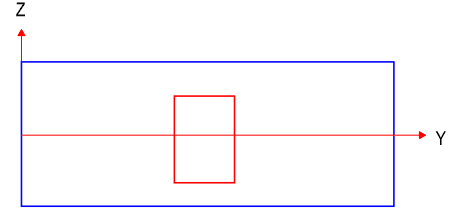
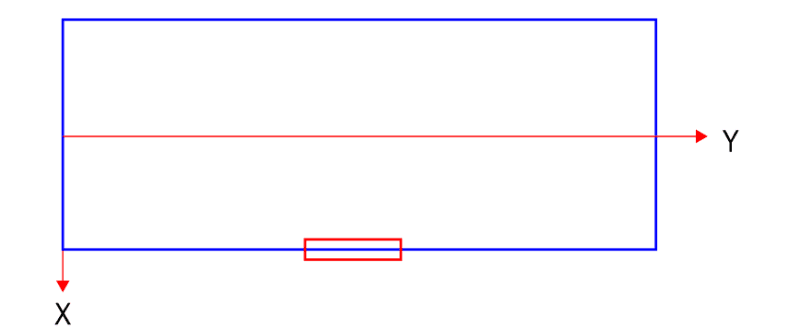
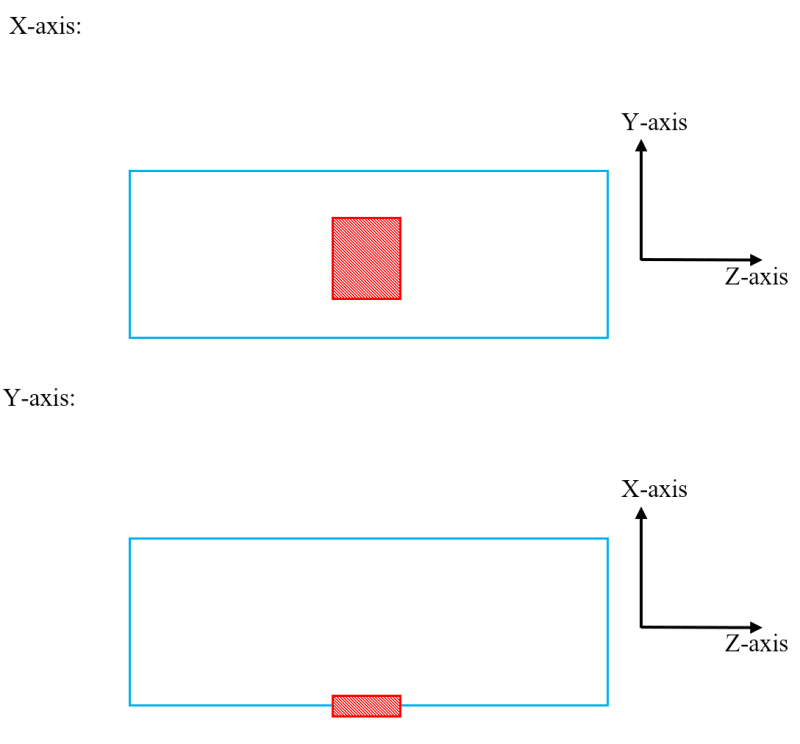
A steel door of 120 kg is bolted to the right side of the steel pipe, in the middle. Can you please help me with calculating the centre of gravity?
Please see attached image.
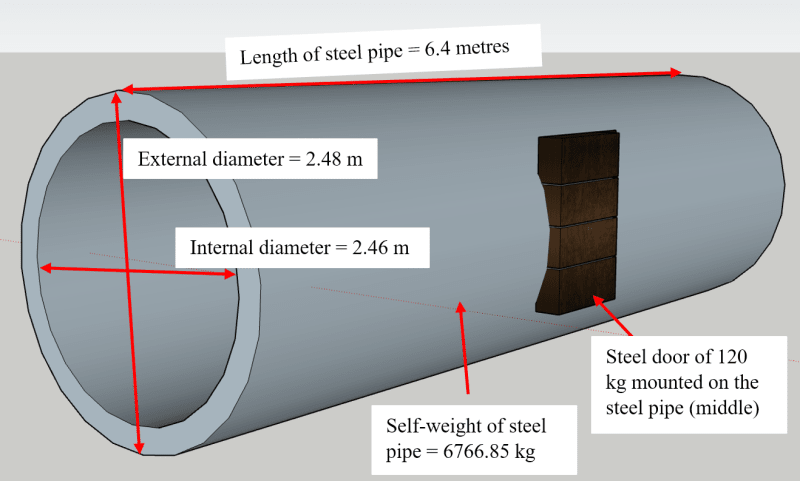
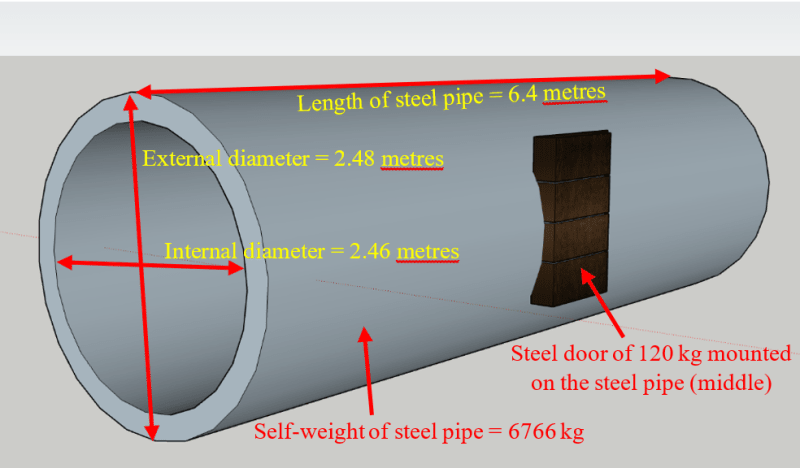
I have a steel pipe with the dimensions shown below:
Length of the pipe = 6.4 metres.
External diameter = 2.48 metres.
Internal diameter = 2.46 metres.
Self-weight of the steel pipe = 6766.85 kg (uniform steel pipe).
A steel door of 120 kg is bolted to the right side of the steel pipe, in the middle. Can you please help me with calculating the centre of gravity?
Please see attached image.