IEC 60287-1-3:2002 Annex A - Calcuation of impedances 1

If you know how Table A1 is built then see attached one example

Here attached calculation of the reactance shown in Table A2 first column.

Actually, when the reactance is calculated the distances for i and i+1 from table A1 are not the same for conductors as for shields .I added a column to indicate this order.

Hi

Thanks a lot for your responses.

I still dont understand table A.1.

In the formula for Xi,k, the LN function is LN(di+1,k/di,k), how can i=1, k=1 be equal to R2R1 ie. 1000 and not 12.73?

Thanks

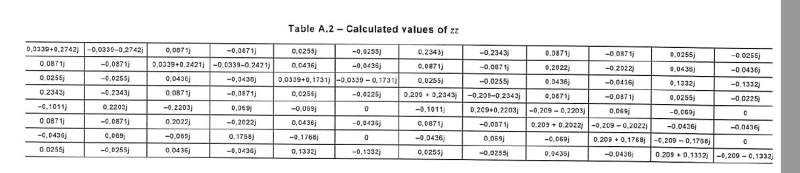
The author of the standard does not explain why the reactance is so calculated.
However, if we take other publication like EPRI EL-5036-V4 Appendix A
the voltage of A phase will be
EAn=Ia1(RA1+jXA1)+IA2(jXA1-A2)+IB1*(jXA1-B1)...+IA(RL+jXL) where:
RA1=A1conductor resistance
XA1=A1conductor self reactance=LA1*0.023/1000*(K'+LN(1/rc))
XA1-A2 =mutual reactance A1-A2=LA1*0.023/1000*(LN(1/DA1-A2))
rc= conductor radius[inches]
We can write (K'+LN(1/rc))=LN(1/α/rc) and if K’=0.25 (K'+LN(1/rc))= 0.687468
and (1/α/rc)=exp(0.687468)= 1.988674 and α=0.7788 for solid conductor.
For 127 wires then α*rc=32.8/2*0.776=12.73 mm.
For sheath-since it is not a stranded wires conductor no need α then- the distance will be 48/2=24
EA1n=IA1(RA1+jXA1)+IA2(jXA1-A2)+IB1*(jXA1-B1)...+IA(RL+jXL) for conductor A1
EA2n=IA2(RA2+jXA2)+IA1(jXA1-A2)+IB1*(jXA2-B1)...+IA(RL+jXL) for conductor A2
But EA1n=EA2n then EA1n-EA2n=0
0=IA1(RA1+jXA1-jXA1-A2)-IA2(RA2+jXA2-jXA1-A2)+IB1[(jXA1-B1)+j(XA2-B1)]....
(RA1+jXA1-jXA1-A2)=RA1+jK*LN(1/(α*rc)-jK*LN(1/DA1-A2)
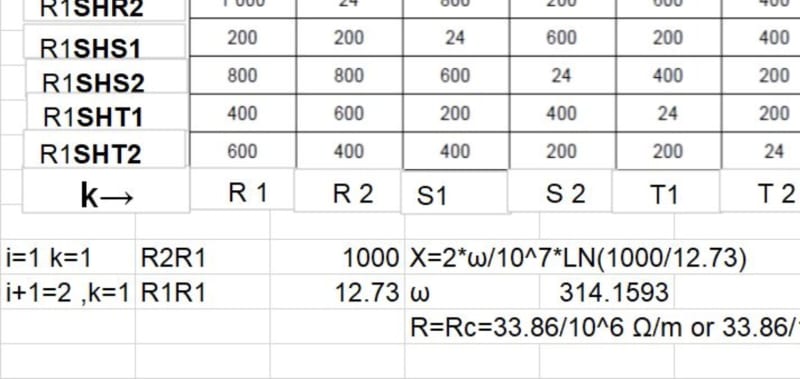
if for i=1 and k=1 we put α*rc and for i=i+1=2 k=1 we put DA1-A2 then we get Xi,k=K*LN(DA1-A2/(α*rc))
then on pos.1 we get RA1+j*K*ln(1000/12.72) where K=2*ω/10^7.