Hi all,
Let's say I have a material that is heated to a initial temperature. We can assume that the material is lumped system (according to the Biot number calculation).
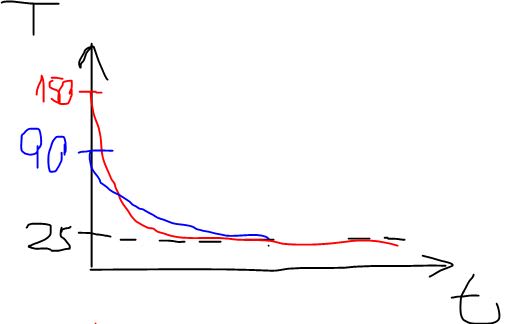
The material was heated and now its sits next to an air conditioner, which helps the cooling down to the room temperature: 25[c].
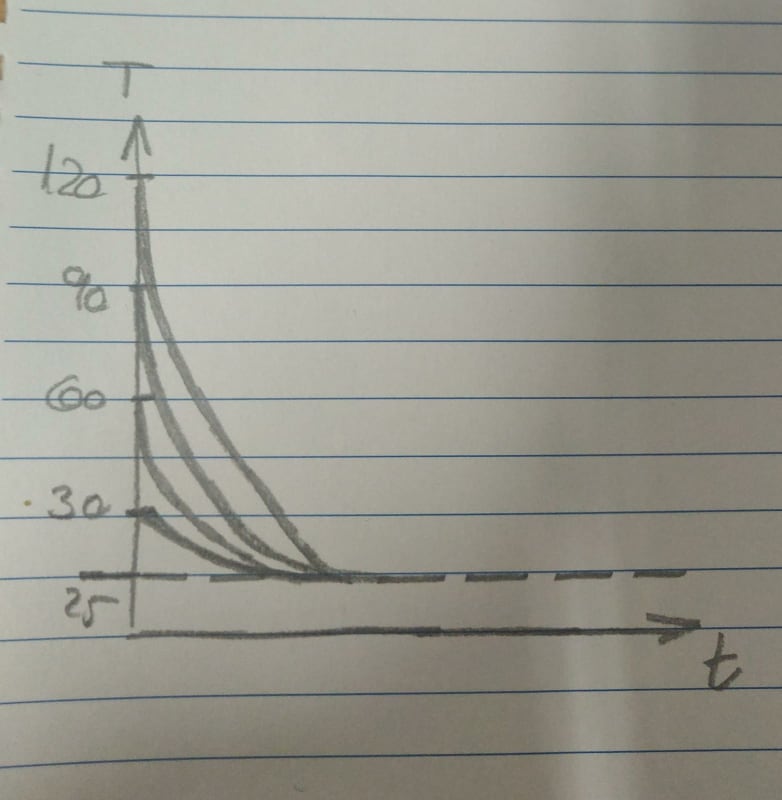
I want to check 5 different cases where the difference in each case is only the initial temperature.
For example: 30 [c], 60 [c], 90[c], 120[c] and 150[c].
The final temperature is the same in all of the cases (25[c]), the physical properties don't change either.
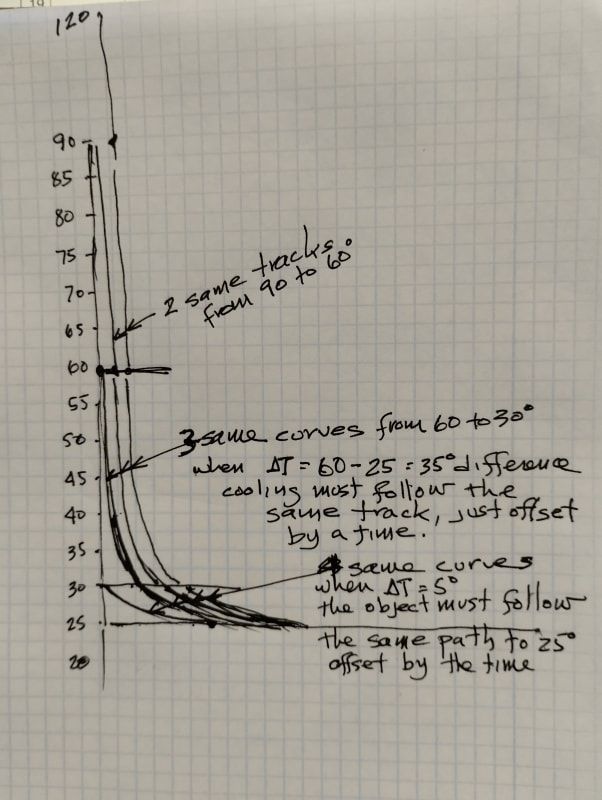
1. I would expect that the higher the initial temperature is then the bigger the difference will be (30-25, 60-25, 90-25, etc) so it would take more time to cool. Is this a correct expectation? Is there a corelation(linear?) between the initial temperature and the time it will take?
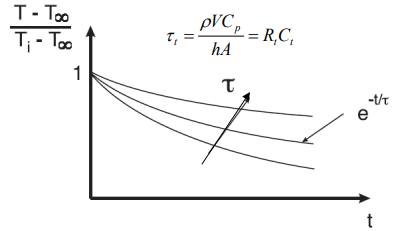
2. I know this equation for lumped systems.
If I make graphs for the 5 cases and place them all on the same plot. Is there a way to compare them? The factor Tau is a constant and doesn't change. Tau isn't depending on the initial temperature, but the Y axis is.
On the other hand, this graph is normalized so that every graph starts from 1.
So how is it possible to compare the rate between the five cases?
Thanks in advance!
Let's say I have a material that is heated to a initial temperature. We can assume that the material is lumped system (according to the Biot number calculation).
The material was heated and now its sits next to an air conditioner, which helps the cooling down to the room temperature: 25[c].
I want to check 5 different cases where the difference in each case is only the initial temperature.
For example: 30 [c], 60 [c], 90[c], 120[c] and 150[c].
The final temperature is the same in all of the cases (25[c]), the physical properties don't change either.
1. I would expect that the higher the initial temperature is then the bigger the difference will be (30-25, 60-25, 90-25, etc) so it would take more time to cool. Is this a correct expectation? Is there a corelation(linear?) between the initial temperature and the time it will take?
2. I know this equation for lumped systems.
If I make graphs for the 5 cases and place them all on the same plot. Is there a way to compare them? The factor Tau is a constant and doesn't change. Tau isn't depending on the initial temperature, but the Y axis is.
On the other hand, this graph is normalized so that every graph starts from 1.
So how is it possible to compare the rate between the five cases?
Thanks in advance!